题目内容
11.在△ABC中,内角A,B,C所对应的边分别为a,b,c,若bsinA-$\sqrt{3}$acosB=0,且a,b,c成等比数列,则$\frac{a+c}{b}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
分析 由结合整理定理代入即可求得tanB=$\sqrt{3}$,求得B,由等比中项可知,b2=ac,根据余弦定理代入即可求得4b2=(a+c)2,即可$\frac{a+c}{b}$的值.
解答 解:由正弦定理可知:$\frac{a}{sinA}=\frac{b}{sinB}$=2R,
∴a=2RsinA,b=2RsinB,
∴bsinA-$\sqrt{3}$acosB=2RsinBsinA-2$\sqrt{3}$RsinAcosB=0,
∵sinA≠0,
∴tanB=$\sqrt{3}$,
∵B∈(0,π),
B=$\frac{π}{3}$,
由a,b,c成等比数列,b2=ac,
∴b2=a2+c2-2accosB=a2+c2-ac,
∴4b2=(a+c)2,
$\frac{a+c}{b}$=2,
故答案选:2.
点评 本题考查正弦定理和余弦定理在解三角形的应用,考查灵活变形能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
6.下列函数中,在[-1,0]上单调递减的是( )
| A. | y=cosx | B. | y=-|x-1| | C. | y=log${\;}_{\frac{1}{2}}}$$\frac{2-x}{2+x}$ | D. | y=ex+e-x |
16.在极坐标系中,与点(3,-$\frac{π}{3}$)关于极轴所在直线对称的点的极坐标是( )
| A. | (3,$\frac{2π}{3}$) | B. | (3,$\frac{π}{3}$) | C. | (3,$\frac{4π}{3}$) | D. | (3,$\frac{5π}{6}$) |
13.△ABC的三个内角分别记为A,B,C,若tanAtanB=tanA+tanB+1,则cosC的值是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
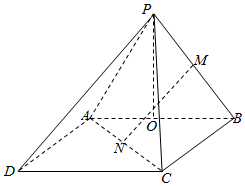 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,