题目内容
已知0<a<
,sinα=
(1)求
的值;
(2)求tan(α-
)的值.
| π |
| 2 |
| 4 |
| 5 |
(1)求
| sin2α+sin2α |
| cos2α+cos2α |
(2)求tan(α-
| 5π |
| 4 |
(1)∵0<a<
,sinα=
,∴cosα=
=
.
∴
=
=
=20;
(2)由(1)可知:tanα=
=
.
∴tan(α-
)=tan(α-
)=
=
=
.
| π |
| 2 |
| 4 |
| 5 |
| 1-sin2α |
| 3 |
| 5 |
∴
| sin2α+sin2α |
| cos2α+cos2α |
| sin2α+2sinαcosα |
| cos2α+2cos2α-1 |
(
| ||||||
3×(
|
(2)由(1)可知:tanα=
| sinα |
| cosα |
| 4 |
| 3 |
∴tan(α-
| 5π |
| 4 |
| π |
| 4 |
tanα-tan
| ||
1+tanαα•tan
|
| ||
1+
|
| 1 |
| 7 |

练习册系列答案
相关题目
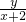 的取值范围;
的取值范围;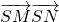 的最小值.
的最小值.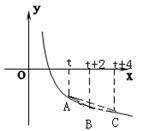 ①、记△ABC的面积为S,求出S=f(t)的表达式;并判断出S== f(t)的单调性;
①、记△ABC的面积为S,求出S=f(t)的表达式;并判断出S== f(t)的单调性;