Question

已知两定点A（-2，0），B（1，0），动点P（x，y）满足|PA|=2|PB|．
（1）求动点P的轨迹C的方程；
（2）求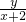的取值范围；
（3）设点S在过点A且垂直于x轴的直线l上运动，作SM，SN与轨迹C相切（M，N为切点）．
①求证：M，B，N三点共线；
②求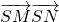的最小值．

Answer 1

解：（1）已知两定点A（-2，0），B（1，0），如果动点P满足|PA|=2|PB|，设P点的坐标为（x，y），
则（x+2）²+y²=4[（x-1）²+y²]，即（x-2）²+y²=4，
所以点的轨迹是以（2，0）为圆心，2为半径的圆，
（2）表示P（x，y）与定点（-2，0）所连直线的斜率
而点P（x，y）在圆（x-2）²+y²=4，上运动，
设即y=k（x+2），即kx-y+2k=0，圆心（2，0）到此直线的距离为：
d=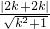，令d=2得?k=±，
结合图形易求得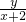的取值范围为[-，]．
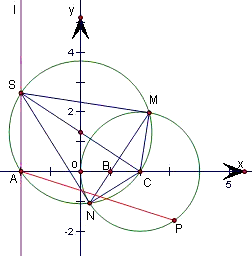
（3）①如图，由题意知直线MN可看成是以SC为直径的圆与圆C的公共弦所在的直线，
设S（-2，t），C（2，0），则以SC为直径的圆的方程为：
x²+（y-）²=2²+（0-）²即x²+y²-ty-4=0，又（x-2）²+y²=4
两者作差，得：4x-ty-4=0，此方程即为直线MN的方程，
令y=0得x=1，即直线MN过点B（1，0），
从而M，B，N三点共线；
②=
=
=
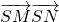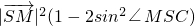
设SC=m，由于MC=2，且m≥4，
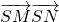∴=m²+-12，此函数在m≥4时是单调增函数，
当且仅当m=4时，它取得最小值，最小值为：m²+-12=4²+-12=6．
故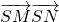的最小值6．
分析：（1）设P点的坐标为（x，y），用坐标表示|PA|、|PB|，代入等式|PA|=2|PB|，整理即得点P的轨迹方程；
（2）利用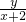的几何意义，转化为P（x，y）与定点（-2，0）所连直线的斜率，故易求．
（3）①如图，由题意知直线MN可看成是以SC为直径的圆与圆C的公共弦所在的直线，利用两圆的方程的差求得直线MN的方程，从而证得直线MN过点B（1，0），从而M，B，N三点共线；
②由于===
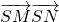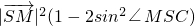设SC=m，从而建立函数关系式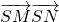=m²++4，此函数在m≥4时是单调增函数，从而求出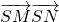的最小值．
点评：本题考查轨迹方程、三点共线、平面向量数量积的运算等．本题求轨迹的方法是利用的是直接法，直接法是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程．