题目内容
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e∈[$\sqrt{2}$,2],则其渐近线的倾斜角的取值范围是( )| A. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{3π}{4}$] | B. | [$\frac{π}{6}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{6}$] | C. | [$\frac{π}{6}$,$\frac{π}{4}$]∪[$\frac{4π}{3}$,$\frac{5π}{6}$] | D. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{5}$] |
分析 利用双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e∈[$\sqrt{2}$,2],求得1≤$\frac{b}{a}$≤$\sqrt{3}$,-$\sqrt{3}$≤-$\frac{b}{a}$≤-1,即可得到所求范围.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率e∈[$\sqrt{2}$,2],
∴$\sqrt{2}$≤$\frac{c}{a}$≤2,
∴2≤1+$\frac{{b}^{2}}{{a}^{2}}$≤4,
∴1≤$\frac{b}{a}$≤$\sqrt{3}$,-$\sqrt{3}$≤-$\frac{b}{a}$≤-1,
∴渐近线的倾斜角的取值范围是[$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{3π}{4}$].
故选:A.
点评 本题考查双曲线的方程和性质,主要考查渐近线方程的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
2.已知正方体ABCD-A1B1C1D1的棱长是3,线段MN的长是2,M在DD1上运动,N在平面ABCD上运动,则M,N的中点P形成的曲面与ABCD面,DCC1D1面,ADD1A1面所围成的几何体的体积是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
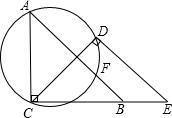 已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.
已知,如图∠A=45°,∠ACE=∠CDE=90°,点B在CE上,CB=CD,过A、C、D三点的圆交AB于点F,求证:点F是△CDE的内心.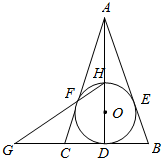 如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.
如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.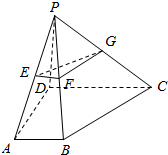 如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.
如图,四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}AD$=1.