Question

（05年江西卷理）（14分）

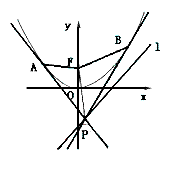
如图，设抛物线的焦点为F，动点P在直线上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.

（1）求△APB的重心G的轨迹方程.

（2）证明∠PFA=∠PFB.

 

Answer 1

解析：（1）设切点A、B坐标分别为，

∴切线AP的方程为：

  切线BP的方程为：

解得P点的坐标为：

所以△APB的重心G的坐标为 ，

所以，由点P在直线l上运动，从而得到重心G的轨迹方程为：

   （2）方法1：因为

由于P点在抛物线外，则

∴

同理有

∴∠AFP=∠PFB.

方法2：①当所以P点坐标为，则P点到直线AF的距离为：

即

所以P点到直线BF的距离为：

所以d₁=d₂，即得∠AFP=∠PFB.

②当时，直线AF的方程：

直线BF的方程：

所以P点到直线AF的距离为：

，同理可得到P点到直线BF的距离，因此由d₁=d₂，可得到∠AFP=∠PFB.