题目内容
已知向量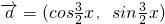 ,
,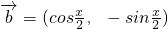 ,x
,x .
.
(1)求 及|
及| |;
|;
(2)求函数f(x)=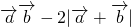 值域.
值域.
解:(1) =cos
=cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x=cos(
x=cos( x+
x+ x)=cos2x.
x)=cos2x.
∵( )2=(cos
)2=(cos x+cos
x+cos x)2+(sin
x)2+(sin x-sin
x-sin x)2=2+2(cos
x)2=2+2(cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x)
x)
=2+2cos2x=2+2(2cos2x-1)=4cos2x
且x∈[0, ]
]
∴| |=2cosx.
|=2cosx.
(2)由(1)知f(x)=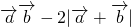 =cos2x-4cosx
=cos2x-4cosx
=2cos2x-4cosx-1=2(cosx-1)2-3
∵x∈[0, ]∴cosx∈[0,1]
]∴cosx∈[0,1]
∴函数f(x)=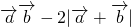 值域是[-3,-1].
值域是[-3,-1].
分析:(1)由向量数量积的坐标公式,及余弦的差角公式可求出 •
• ;因为|
;因为| |2=(
|2=( )2,所以先求(
)2,所以先求( )2,然后求|
)2,然后求| |.
|.
(2)由 •
• 与|
与| |求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.
|求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.
点评:有的三角函数问题,不能转化为正弦型函数y=Asin(ωx+φ)+B(或余弦型函数y=Acos(ωx+φ)+B)的形式来解决,可考虑利用二次函数来处理.
 =cos
=cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x=cos(
x=cos( x+
x+ x)=cos2x.
x)=cos2x.∵(
 )2=(cos
)2=(cos x+cos
x+cos x)2+(sin
x)2+(sin x-sin
x-sin x)2=2+2(cos
x)2=2+2(cos x•cos
x•cos x-sin
x-sin x•sin
x•sin x)
x)=2+2cos2x=2+2(2cos2x-1)=4cos2x
且x∈[0,
 ]
]∴|
 |=2cosx.
|=2cosx.(2)由(1)知f(x)=
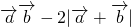 =cos2x-4cosx
=cos2x-4cosx=2cos2x-4cosx-1=2(cosx-1)2-3
∵x∈[0,
 ]∴cosx∈[0,1]
]∴cosx∈[0,1]∴函数f(x)=
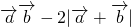 值域是[-3,-1].
值域是[-3,-1].分析:(1)由向量数量积的坐标公式,及余弦的差角公式可求出
 •
• ;因为|
;因为| |2=(
|2=( )2,所以先求(
)2,所以先求( )2,然后求|
)2,然后求| |.
|.(2)由
 •
• 与|
与| |求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.
|求出f(x),然后把它整理为二次函数形式,进而结合余弦的值域解决问题.点评:有的三角函数问题,不能转化为正弦型函数y=Asin(ωx+φ)+B(或余弦型函数y=Acos(ωx+φ)+B)的形式来解决,可考虑利用二次函数来处理.

练习册系列答案
相关题目
