题目内容
(本小题共12分）
在平面直角坐标系中，已知向量a=（
x，y+1），向量b=（x，y—1），a⊥b,动点M
（x，y）的轨迹为E。
（Ⅰ）证明：存在圆心在原点的圆，使得该圆的任意一条切线与轨迹E恒有两个交点
A、B，且OA⊥OB（O为坐标原点），并求出该圆的方程；
（Ⅱ）设直线l与圆C：x
+y=R（1＜R＜2）相切于A
，且l与轨迹E只有一个
公共点B，当R为何值时，| AB|取得最大值？并求出最大值。
（Ⅰ）由
得
∴M轨迹E的方程为
…………1分
设圆的切线y=kx+t,代入x2+4y2=4得（1+4k2）x2+8ktx+4(t2-1)=0
直线与圆两交点A（x1，y1）,B（x2,y2）
则△＞0，t2＜4k2+1 ①
又由
得x1x2+y1y2=0可得5t2=4(k2+1) ②
②代入① 4(k2+1) ＜20k2+5恒成立………………4分
又由
得：
故所求圆的方程为
…………5分
当切线斜率k不存在时，切线为
与椭圆x2+4y2=4交于
也满足
综合上述所求圆为…………6分
（Ⅱ）直线l:y=kx+t，圆x2+y2=R2切于A1，则
∴t2=R2(1+k2) ③
又l与椭圆x2+4y2=4有唯一公共点B1
∴
有唯一解
∴△=0，即4k2-t2+1=0 ④
由③④得
当仅当
时
………………12分
练习册系列答案
优加精卷系列答案
相关题目
的焦点坐
标为
（
），点M（
，
）在椭圆E上
（1）求椭圆E的方程；（2）O为坐标原点，⊙
的任意一条切线与椭圆E有两个交点
，
且
，求⊙
⊥平面
，
∥
是正三角形，
，且
是
的中点
∥平面
；
．
名，女同学有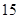
名，老师按照分层抽样的方法组建了一个
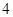人的课外兴趣小组．
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
，
，求证：
.
的值.