题目内容
14.在正方体ABCD-A1B1C1D1中,下列几种说法不正确的是( )| A. | A1C1⊥BD | B. | D1C1∥AB | ||
| C. | 二面角A1-BC-D的平面角为45° | D. | AC1与平面ABCD所成的角为45° |
分析 作出图形,逐项分析,
解答 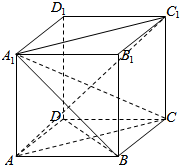 解:对于A,连接AC,则AC⊥BD,A1C1∥AC,∴A1C1⊥BD,故A正确;
解:对于A,连接AC,则AC⊥BD,A1C1∥AC,∴A1C1⊥BD,故A正确;
对于B,∵D1C1∥DC,DC∥AB,∴D1C1∥AB,故B正确;
对于C,∵BC⊥平面A1ABB1,A1B?平面A1ABB1,∴BC⊥A1B,
∵AB⊥BC,平面A1BC∩平面BCD=BC,A1B?平面A1BC,AB?平面BCD,
∴∠ABA1是二面角A1-BC-D的平面角,
∵△A1AB是等腰直角三角形,∴∠ABA1=45°,故C正确;
对于D,∵C1C⊥平面ABCD,AC1∩平面ABCD=A,
∴∠C1AC是AC1与平面ABCD所成的角,∵AC≠C1C,∴∠C1AC≠45°,故D错误.
故选D.
点评 本题考查了线面的空间位置关系及空间角,做出图形分析是关键.

练习册系列答案
相关题目
5.证明:设m是任一正整数,则am=$\frac{1}{2}$$+\frac{1}{3}$$+\frac{1}{4}$+$\frac{1}{5}$+…+$\frac{1}{{2}^{m}}$不是整数.
9.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
| A. | ∠ADE=20° | B. | ∠ADE=30° | C. | ∠ADE=$\frac{1}{3}$∠ADC | D. | ∠ADE=$\frac{1}{2}$∠ADC |
3.在下列各组函数中,f(x)与g(x)表示同一函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | y=x与y=$\sqrt{{x}^{2}}$ | C. | y=x2与y=(x+1)2 | D. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ |
4.若函数y=f(x)为偶函数,且在(0,+∞)上是减函数,又f(3)=0,则$\frac{f(x)+f(-x)}{2x}<0$的解集为( )
| A. | (-3,3) | B. | (-3,0)∪(3,+∞) | C. | (-∞,-3)∪(0,3) | D. | (-∞,-3)∪(3,+∞) |