Question

【题目】如图，线段AB在平面α内，线段BD⊥AB，线段AC⊥α，且AB= ，AC=BD=12，CD= ，求线段BD与平面α所成的角．

Answer 1

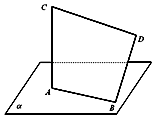
【答案】解：以点A为原点建立坐标系， 得到下列坐标：A（0，0，0），B（0， ，0），C（0，0，12），设D（x，y，z），
∵ ，∴ ，
又 ，
解得： ．
∴ ，
因此线段BD与平面α所成的角等于900﹣θ=300 ．

【解析】由题意建立空间直角坐标系，结合已知求出所用点的坐标，求出异面直线AC与BD所成角，得到线段BD与平面α所成的角．
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识，掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则．