题目内容

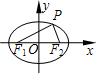如图，设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点为F1，F2，P为椭圆上的点，且
PF1
•
PF1
•
PF2
=0；如果△PF1F2的面积为
1
3
a2，那么该椭圆的离心率为
6
3
6
3
．
分析：利用
PF1
•
PF2
=0，可知
PF1
⊥
PF2
，结合椭圆的定义，及△PF1F2的面积，可求几何量之间的关系，从而可求离心率．
解答：解：由题意，∵
PF1
•
PF2
=0，∴
PF1
⊥
PF2

设PF1=m，PF2=n
∴
1
2
mn=
1
3
a2
m2+n2=4c2
m+n=2a

∴e2=
2
3

∴e=
6
3

故答案为：
6
3
．
点评：本题的考点是椭圆的简单性质，主要考查椭圆的定义，考查椭圆的离心率，关键是找出几何量之间的关系．
练习册系列答案
相关题目
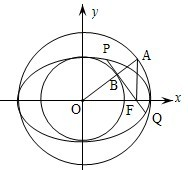精英家教网如图，以椭圆
x2
a2
+
y2
b2
=1 (a＞b＞0)的中心O为圆心，分别以a和b为半径作大圆和小圆．过椭圆右焦点F（c，0）（c＞b）作垂直于x轴的直线交大圆于第一象限内的点A．连接OA交小圆于点B．设直线BF是小圆的切线．
（1）求证c2=ab，并求直线BF与y轴的交点M的坐标；
（2）设直线BF交椭圆于P、Q两点，求证
OP
•
OQ
=
1
2
b2．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，其长轴长与短轴长的和等于6．
（1）求椭圆E的方程；
（2）如图，设椭圆E的上、下顶点分别为A1、A2，P是椭圆上异于A1、A2的任意一点，直线PA1、PA2分别交x轴于点N、M，若直线OT与过点M、N的圆G相切，切点为T．证明：线段OT的长为定值．
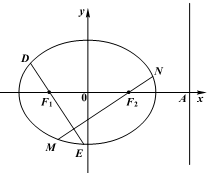（2011•天津模拟）设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的焦点分别为F1（-1，0）、F2（1，0），直线l：x=a2交x轴于点A，且
AF1
=2
AF2
．
（Ⅰ）试求椭圆的方程；
（2）过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点（如图所示），若四边形DMEN的面积为
27
7
，求DE的直线方程．
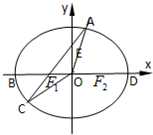精英家教网（A题）如图，在椭圆
x2
a2
+
y2
8
=1（a＞0）中，F1，F2分别是椭圆的左右焦点，B，D分别为椭圆的左右顶点，A为椭圆在第一象限内弧上的任意一点，直线AF1交y轴于点E，且点F1，F2三等分线段BD．
（1）若四边形EBCF2为平行四边形，求点C的坐标；
（2）设m=
S△AF1O
S△AEO
，n=
S△CF1O
S△CEO
，求m+n的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网