Question

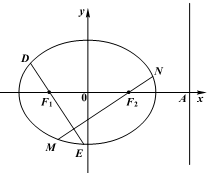（2011•天津模拟）设椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦点分别为F₁（-1，0）、F₂（1，0），直线l：x=a²交x轴于点A，且

AF1

=2

AF2

．
（Ⅰ）试求椭圆的方程；
（2）过F₁、F₂分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点（如图所示），若四边形DMEN的面积为

27

7

，求DE的直线方程．

Answer 1

分析：（I）由已知中椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦点分别为F₁（-1，0）、F₂（1，0），x=a²交x轴于点A，且

AF1

=2

AF2

，可得F₂为AF₁的中点，进而求出a²，b²的值后可得椭圆的方程．
（II）分析讨论直线DE与x轴垂直和MN与x轴垂直及直线DE，MN均与x轴不垂直时，满足四边形DMEN的面积为

27

7

的条件，进而得到DE的直线方程．

解答：解：（Ⅰ）∵椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦点分别为F₁（-1，0）、F₂（1，0），
∴|

F1F2

|=2c=2，
∴c=1
∵直线l：x=a²交x轴于点A，
∴A（a²，0）----------（1分）
∵

AF1

=2

AF2

∴F2为AF₁的中点------------（2分）
∴a²=3，b²=2------------（3分）
即：椭圆方程为

x2

3

+=1------------（4分）
（2）当直线DE与x轴垂直时，|DE|=2

b2

a

=

4

3

，此时|MN|=2a=2

3

，
四边形DMEN的面积S=

|DE|•MN|

2

=4不符合题意故舍掉；------------（5分）
同理当MN与x轴垂直时，也有四边形DMEN的面积积S=

|DE|•MN|

2

=4不符合题意故舍掉；------------（6分）
当直线DE，MN均与x轴不垂直时，
设DE：y=k（x+1），
代入消去y得：（2+3k²）x²+6k²x+（3k²-6）=0------------（7分）
设D（x₁，y₁）、E（x₂，y₂），则

x1+x2= -6k2 2+3k2 x1•x2= 3k2-6 2+3k2

------------（8分）
所以|x₁-x₂|=

(x1+x2)2-4x1x2

=

4 3 • k2+1

2+3k2

，------------（9分）
所以|DE|=

k2+1

•|x₁-x₂|=

4 3 •(k2+1)

2+3k2

，------------（10分）
同理|MN|=

4 3 •[(- 1 k )2+1]

2+3(- 1 k )2

=

4 3 •( 1 k2  +1)

2+ 3 k2

------------（12分）
所以四边形的面积S=

|DE|•|MN|

2

=

1

2

•

4 3 •(k2+1)

2+3k2

•

4 3 •( 1 k2  +1)

2+ 3 k2

=

24(k2+ 1 k2 +2)

6(k2+ 1 k2 )+13

由S=

27

7

⇒k2=2或k²=

1

2

⇒k=±

2

，k=±

2

2

，
所以直线l_DE：

2

x-y+

2

=0或l_DE：

2

x+y+

2

=0或l_DE：

2

x-2y+

2

=0或l_DE：

2

x+2y+

2

=0-------（14分）

点评：本题考查的知识点是直线与圆锥曲线的综合问题，椭圆的标准方程，其中根据已知条件求出椭圆的标准方程是解答本题的关键．