Question

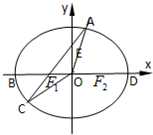（A题）如图，在椭圆

x2

a2

+

y2

8

=1（a＞0）中，F₁，F₂分别是椭圆的左右焦点，B，D分别为椭圆的左右顶点，A为椭圆在第一象限内弧上的任意一点，直线AF₁交y轴于点E，且点F₁，F₂三等分线段BD．
（1）若四边形EBCF₂为平行四边形，求点C的坐标；
（2）设m=

S△AF1O

S△AEO

，n=

S△CF1O

S△CEO

，求m+n的取值范围．

Answer 1

分析：（1）由F₁，F₂三等分线段BD，得|F₁F₂|=

1

3

|BD|，即2c=

1

3

•2a①，又a²=b²+c²②，b²=8③，联立方程组即可求得a，c值，从而可得F₁坐标为（-1，0），由四边形EBCF₂为平行四边形及F₁为BF₂的中点，知F₁为CE中点，即C、E关于点F₁对称，设C（x₀，y₀），则E（-2-x₀，-y₀），根据C在椭圆上及E在y轴上可得关于x₀的方程组，由此可求得C点坐标；
（2）易知直线AC存在斜率，设直线AC：y=k（x+1），A（x₁，y₁），C（x₂，y₂），由

x2 9 + y2 8 =1 y=k(x+1)

，得（8+9k²）x²+18k²x+9（k²-8）=0，x1+x2=-

18k2

8+9k2

，x1x2=

9(k2-8)

8+9k2

，
则m+n=

S△AF1O

S△AEO

+

S△CF1O

S△CEO

=

1 2 |AF1|h

1 2 |AE|h

+

1 2 |CF1|h

1 2 |CE|h

=

|AF1|

|AE|

+

|CF1|

|CE|

，利用弦长公式及韦达定理可把m+n表示为关于k的函数，由点A在第一象限可求得k的取值范围，根据k的范围即可求得m+n的取值范围；

解答：解：（1）因为F₁，F₂三等分线段BD，所以|F₁F₂|=

1

3

|BD|，即2c=

1

3

•2a，所以a=3c①，
又a²=b²+c²②，b²=8③，联立①②③解得a=3，c=1，
所以B（-3，0），F₁（-1，0），F₁为BF₂的中点，
因为四边形EBCF₂为平行四边形，所以C，E关于F₁（-1，0）对称，
设C（x₀，y₀），则E（-2-x₀，-y₀），
因为E在y轴上，所以-2-x₀=0，解得x₀=-2，
又因为点C（x₀，y₀）在椭圆上，所以

x02

9

+

y02

8

=1，
又x₀=-2，所以

4

9

+

y02

8

=1，解得y₀=±

2 10

3

，依题意y0=-

2 10

3

，
因此点C的坐标为（-2，-

2 10

3

）；
（2）依题意直线AC的斜率存在，所以可设直线AC：y=k（x+1），A（x₁，y₁），C（x₂，y₂），
由

x2 9 + y2 8 =1 y=k(x+1)

，得（8+9k²）x²+18k²x+9（k²-8）=0，x1+x2=-

18k2

8+9k2

，x1x2=

9(k2-8)

8+9k2

，
所以m=

S△AF1O

S△AEO

=

1 2 |AF1|h

1 2 |AE|h

=

|AF1|

|AE|

=

1+k2 •|-1-x1|

1+k2 •|0-x1|

=

|x1+1|

|x1|

=

x1+1

x1

，其中h为点O到AE的距离，
n=

S△CF1O

S△CEO

=

1 2 |CF1|h

1 2 |CE|h

=

|CF1|

|CE|

=

1+k2• |-1-x2|

1+k2 •|0-x2|

=

|1+x2|

|x2|

=

-1-x2

-x2

=

1+x2

x2

，
m+n=

x1+1

x1

+

1+x2

x2

=

x2(1+x1)+x1(1+x2)

x1x2

=

2x1x2+x1+x2

x1x2

，
=2+

x1+x2

x1x2

=2+

-18k2 8+9k2

9(k2-8) 8+9k2

=2+

-2k2

k2-8

=2-

2(k2-8)+16

k2-8

=-

16

k2-8

．
因为点A在第一象限，所以0＜k＜2

2

，即0＜k²＜8，
令t=-

16

k2-8

，则k2=8-

16

t

，所以0＜8-

16

t

＜8，即0＜

1

t

＜

1

2

，解得t＞2，
故m+n的取值范围是t＞2．

点评：本题考查直线与圆锥曲线的位置关系、椭圆方程的求解，考查函数思想，考查学生综合运用所学知识分析问题解决问题的能力，解决（2）问的关键是把m+n表示为关于直线AC斜率k的函数，体现函数思想．