题目内容
已知各项均不为零的数列{an}，定义向量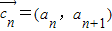
，
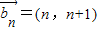，n∈N*．下列命题中真命题是（ ）A．若?n∈N*总有
∥
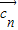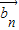成立，则数列{an}是等差数列B．若?n∈N*总有
∥
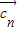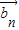成立，则数列{an}是等比数列C．若?n∈N*总有
⊥
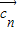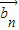成立，则数列{an}是等差数列D．若?n∈N*总有
⊥
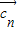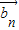成立，则数列{an}是等比数列
【答案】分析：由题意根据向量平行的坐标表示可得nan+1=（n+1）an．⇒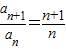
⇒an=na1，从而可进行判断．
解答：解：由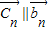
可得，nan+1=（n+1）an，即
，
∴
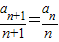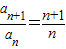
于是an=na1，
故选A
点评：本题主要考查了向量平行的坐标表示，等差及等比数列的判断，属于基础试题．
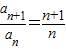⇒an=na1，从而可进行判断．解答：解：由
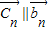可得，nan+1=（n+1）an，即，∴
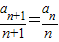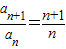
于是an=na1，
故选A
点评：本题主要考查了向量平行的坐标表示，等差及等比数列的判断，属于基础试题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
已知各项均不为零的数列{an}，定义向量
=(an，an+1)，
=(n，n+1)，n∈N*．下列命题中真命题是（ ）
| cn |
| bn |
A、若?n∈N*总有
| ||||
B、若?n∈N*总有
| ||||
C、若?n∈N*总有
| ||||
D、若?n∈N*总有
|