题目内容
(本小题满分 分)设函数
分)设函数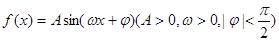 的最高点
的最高点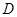 的坐标为(
的坐标为(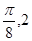 ),由最高点
),由最高点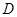 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与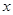 的交点的坐标为(
的交点的坐标为(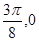 ).
).
(1)求函数 的解析式.
的解析式.
(2)当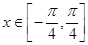 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量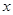 的值.
的值.
(3)将函数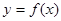 的图象向右平移
的图象向右平移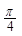 个单位,得到函数
个单位,得到函数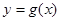 的图象,求函数
的图象,求函数
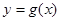 的单调减区间.
的单调减区间.
(1)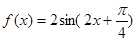
(2)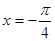 时,函数
时,函数 取得最小值
取得最小值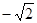 ;
;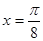 时,函数
时,函数 取得最大值
取得最大值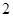
(3)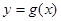 的单调减区间为
的单调减区间为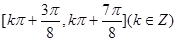
【解析】
试题分析:(1)∵由最高点D(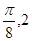 )运动到相邻最低点时,函数图形与
)运动到相邻最低点时,函数图形与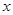 的交点的坐标
的交点的坐标
为(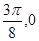 ),
),
∴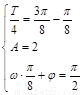 , ……2分
, ……2分
从而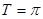 ,
,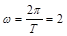 ,
,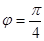 , ……4分
, ……4分
∴函数解析式为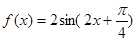 . ……5分
. ……5分
(2)由(1)得函数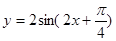 ,
,
当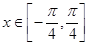 时,
时,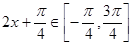 . ……6分
. ……6分
∴当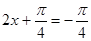 ,即
,即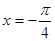 时,函数
时,函数 取得最小值
取得最小值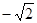 . ……8分
. ……8分
当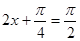 ,即
,即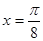 时,函数
时,函数 取得最大值
取得最大值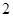 .
……10分
.
……10分
(3)由题意得,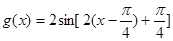 ,即
,即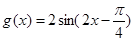 , ……12分
, ……12分
由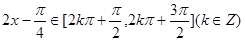 ,
,
得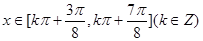 , ……13分
, ……13分
即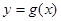 的单调减区间为
的单调减区间为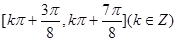 . ……14分
. ……14分
考点:本小题主要考查由三角函数的图象求函数的解析式以及对函数性质如最值、单调区间等的研究,考查学生数形结合思想的应用.
点评:一般来说,由三角函数图象确定解析式时,由最值确定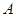 ,由周期确定
,由周期确定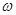 ,由特殊值确定
,由特殊值确定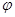 ,知道了函数解析式,求函数的最值和单调区间时要借助三角函数的图象解决问题.
,知道了函数解析式,求函数的最值和单调区间时要借助三角函数的图象解决问题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 的部分图象如图所示:
的部分图象如图所示: 的值;
的值; ,当
,当 时,求函数
时,求函数 的值域.
的值域.
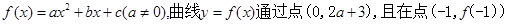
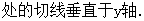
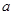 分别表示
分别表示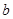 和
和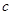 ;
;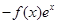 的单调区间。
的单调区间。