题目内容
19.若α是锐角,且cos(α+$\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$,则sinα的值等于( )| A. | $\frac{\sqrt{6}+3}{6}$ | B. | $\frac{\sqrt{6}-3}{6}$ | C. | $\frac{2\sqrt{6}+1}{6}$ | D. | $\frac{2\sqrt{6}-1}{6}$ |
分析 由条件利用同角三角函数的基本关系,两角和差的正弦公式,求得sinα=sin[(α+$\frac{π}{3}$)-$\frac{π}{3}$]的值.
解答 解:α是锐角,且cos(α+$\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$,∴sin(α+$\frac{π}{3}$)=$\frac{\sqrt{6}}{3}$,
则sinα=sin[(α+$\frac{π}{3}$)-$\frac{π}{3}$]=sin(α+$\frac{π}{3}$)cos$\frac{π}{3}$-cos(α+$\frac{π}{3}$)sin$\frac{π}{3}$=$\frac{\sqrt{6}}{3}×\frac{1}{2}$-$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}-3}{6}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,两角和差的正弦公式,属于基础题.

练习册系列答案
相关题目
10.已知tanα+sinα=a(a≠0),tanα-sinα=b,则cosα等于( )
| A. | $\frac{a+b}{2}$ | B. | $\frac{a-b}{2}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{a-b}{a+b}$ |
7.直线y=-$\sqrt{3}$(x-2)截圆x2+y2=4所得的劣弧所对的圆心角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
9.设函数f(x)=(a-1)x+b是R上的减函数,则有( )
| A. | a≥1 | B. | a≤1 | C. | a>-1 | D. | a<1 |
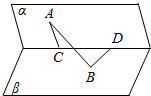 如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求:
如图,二面角α-l-β为60°,点A、B分别为平面α和平面β上的点,点A到l的距离为|AC|=4,点B到l的距离为|BD|=5,|CD|=6,求: