题目内容
7.直线y=-$\sqrt{3}$(x-2)截圆x2+y2=4所得的劣弧所对的圆心角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
分析 先求得弦心距d=$\sqrt{3}$,设所求的圆心角为θ,则有cos$\frac{θ}{2}$=$\frac{d}{r}$,由此求得$\frac{θ}{2}$的值,可得θ的值.
解答 解:直线y=-$\sqrt{3}$(x-2),即$\sqrt{3}$x+y-2$\sqrt{3}$=0,弦心距d=$\frac{|0+0-2\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$,
设直线y=-$\sqrt{3}$(x-2)截圆x2+y2=4所得的劣弧所对的圆心角为θ,则有cos$\frac{θ}{2}$=$\frac{d}{r}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{θ}{2}$=$\frac{π}{6}$,∴θ=$\frac{π}{3}$,
故选:A.
点评 本题主要考查直线和圆相交的性质,点到直线的距离公式的应用,直角三角形中的边角关系,属于基础题.

练习册系列答案
相关题目
17.执行如图所示的程序框图(算法流程图),输出的n为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.等比数列{an}的前n 项和为S n,若an>0,q>1,a3+a5=20,a2a6=64则公比q为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
2.已知双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0)的离心率为$\frac{2\sqrt{3}}{3}$,则m的值为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 3 | C. | 8 | D. | $\frac{\sqrt{3}}{2}$ |
19.若α是锐角,且cos(α+$\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$,则sinα的值等于( )
| A. | $\frac{\sqrt{6}+3}{6}$ | B. | $\frac{\sqrt{6}-3}{6}$ | C. | $\frac{2\sqrt{6}+1}{6}$ | D. | $\frac{2\sqrt{6}-1}{6}$ |
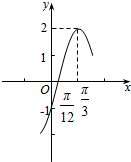 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).


