题目内容
14.若a,b∈R,i为虚数单位,且a+2i=i(b+i),则a+b=1.分析 利用复数相等的充要条件,列出方程组,求解即可.
解答 解:a,b∈R,i为虚数单位,且a+2i=i(b+i),
可得$\left\{\begin{array}{l}a=-1\\ 2=b\end{array}\right.$,
∴a+b=1.
故答案为:1.
点评 本题考查复数的相等的充要条件,考查计算能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
5.对任意非零实数a,b,定义a?b的算法原理如程序框图所示.设a为函数y=x2-2x+3(x∈R)的最小值,b为抛物线y2=8x的焦点到准线的距离,则计算机执行该运算后输出结果是( )
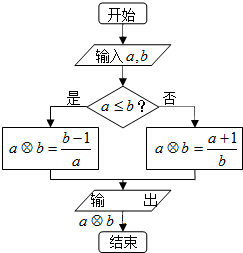

| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{1}{2}$ |
2.已知双曲线$\frac{{x}^{2}}{m}$-y2=1(m>0)的离心率为$\frac{2\sqrt{3}}{3}$,则m的值为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 3 | C. | 8 | D. | $\frac{\sqrt{3}}{2}$ |
19.若α是锐角,且cos(α+$\frac{π}{3}$)=$\frac{\sqrt{3}}{3}$,则sinα的值等于( )
| A. | $\frac{\sqrt{6}+3}{6}$ | B. | $\frac{\sqrt{6}-3}{6}$ | C. | $\frac{2\sqrt{6}+1}{6}$ | D. | $\frac{2\sqrt{6}-1}{6}$ |
3.不等式组$\left\{\begin{array}{l}{{x}^{2}-1<0}\\{{x}^{2}-3x>0}\end{array}\right.$的解集是( )
| A. | {x|-1<x<1} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
4.平面内到两定点F1、F2的距离之比等于常数m(m>0且m≠1)的点的轨迹称为阿波罗尼斯圆,已知曲线C是平面内到两定点F1(-1,0),F2(1,0)距离之比等于常数m(m>0,m≠1)的点的轨迹,下面选项正确的是( )
| A. | 曲线C关于坐标原点对称 | B. | 曲线C关于y轴对称 | ||
| C. | 曲线C关于x轴对称 | D. | 曲线C过坐标原点 |