题目内容
19.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,2).(1)求(2$\overrightarrow{a}$-$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$);
(2)设$\overrightarrow{c}$=(-3,λ),若$\overrightarrow{c}$与$\overrightarrow{a}$夹角为钝角,求λ的值.
分析 (1)向量的坐标运算和向量的数量积的坐标运算计算即可,
(2)若$\overrightarrow{c}$与$\overrightarrow{a}$夹角为钝角,则则$\overrightarrow{c}$•$\overrightarrow{a}$<0,问题得以解决.
解答 解:(1)∵$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,2),
∴2$\overrightarrow{a}$-$\overrightarrow{b}$=(2-2,4-2)=(0,2),2$\overrightarrow{a}$+$\overrightarrow{b}$=(2+2,4+2)=(4,6),
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=0×4+2×6=12;
(2)若$\overrightarrow{c}$与$\overrightarrow{a}$夹角为钝角,则$\overrightarrow{c}$•$\overrightarrow{a}$<0,
$\overrightarrow{c}$•$\overrightarrow{a}$=(-3,λ)•(1,2)=-3+2λ<0,即 λ<$\frac{3}{2}$,
且$\overrightarrow{c}$与$\overrightarrow{a}$不能方向,即-3×2-λ≠0,解得λ≠-6,
故λ的范围为λ>$\frac{3}{2}$,
点评 本题考查了向量的坐标运算和向量的数量积的坐标运算,以及向量的夹角的问题,属于基础题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.已知sinα=$\frac{\sqrt{5}}{5}$,则cos(α-$\frac{π}{4}$)的值为( )
| A. | $\frac{3\sqrt{10}}{10}$ | B. | -$\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$或-$\frac{\sqrt{10}}{10}$ |
10.若a>b,c>d,则下列不等式成立的是( )
| A. | $\frac{a}{c}>\frac{b}{d}$ | B. | ac>bd | C. | a2+c2>b2+d2 | D. | a+c>b+d |
7.某班为了调查同学们周末的运动时间,随机对该班级50名同学进行了不记名的问卷调查,得到了如下表所示的统计结果:
(1)根据统计结果,能否在犯错误概率不超过0.05的前提下,认为该班同学周末的运动时间与性别有关?
(2)用分层抽样的方法,从男生中抽取6名同学,再从这6名同学中随机抽取2名同学,求这两名同学中恰有一位同学运动时间超过2小时的概率.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 运动时间不超过2小时 | 运动时间超过2小时 | 合计 | |
| 男生 | 10 | 20 | 30 |
| 女生 | 13 | 7 | 20 |
| 合计 | 23 | 27 | 50 |
(2)用分层抽样的方法,从男生中抽取6名同学,再从这6名同学中随机抽取2名同学,求这两名同学中恰有一位同学运动时间超过2小时的概率.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
11.红、黄两支队员实力相当的乒乓球队进行擂台赛,已知每支队均有六名队员,规则如下:每支队给队员编号1,2,3,4,5,6,第一场双方1号比赛,负者被淘汰.然后负方队的2号与胜方队的1号再比赛,负者又被淘汰,一直这样进行下去,直到一方队员全被淘汰时,另一方获胜,则红队有3名队员波淘汰且最后战胜黄队的概率是( )
| A. | $\frac{1}{11}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{11}$ |
8.若$\sqrt{3}$sinx-cosx=4-m,则实数m的取值范围是( )
| A. | 2≤m≤6 | B. | -6≤m≤6 | C. | 2<m<6 | D. | 2≤m≤4 |
9.函数f(x)=loga(x3-2ax)(a>0且a≠1)在(4,+∞)上单调递增,则a的取值范围是( )
| A. | 1<a≤4 | B. | 1<a≤8 | C. | 1<a≤12 | D. | 1<a≤24 |
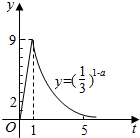 我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线