题目内容
10.若a>b,c>d,则下列不等式成立的是( )| A. | $\frac{a}{c}>\frac{b}{d}$ | B. | ac>bd | C. | a2+c2>b2+d2 | D. | a+c>b+d |
分析 本题是选择题,可采用逐一检验,利用特殊值法进行检验,很快问题得以解决.
解答 解:∵a>b,c>d,
∴设a=1,b=-1,c=-2,d=-5
分别代入选项A、B、C均不符合,
故A、B、C均错,
而选项D正确,
故选:D,
点评 本题主要考查了基本不等式,基本不等式在考纲中是C级要求,本题属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知定义在R上的偶函数f(x),对任意x∈R满足f(x+1)=f(-x+1),当6≤x≤7时,f(x)=1g(x-5);则方程f(x)-1gx=-1+1g5的实数根个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.△ABC的内角A,B,C的对边分别为a,b,c,若sinAsinC=$\frac{1}{4}$,b=$\sqrt{6}$,B=120°,则△ABC的面积等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
5.袋子中装有大小相同的6个小球,分别有2个红球、4个白球,现从中随机摸出3个小球,则至少有2个白球的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{10}$ |
20.在等腰梯形ABCD中,$\overrightarrow{AB}$=-2$\overrightarrow{CD}$,M为BC的中点,则$\overrightarrow{AM}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}$+$\frac{1}{4}\overrightarrow{AD}$ | D. | $\frac{1}{2}\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ |
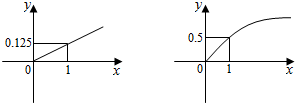 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).