题目内容
定义在R上的奇函数f(x),当x≥0,f(x)=x2-4x
(1)作出函数f(x)的图象;
(2)求函数f(x)的表达式;
(3)求满足方程f(x)=-5的解.
(1)作出函数f(x)的图象;
(2)求函数f(x)的表达式;
(3)求满足方程f(x)=-5的解.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数的图象
专题:函数的性质及应用
分析:(1)根据定义在R上的奇函数f(x)的图象关于原点对称,及x≥0时,f(x)=x2-4x可得到函数f(x)的图象;
(2)当x<0时,-x>0,结合x≥0,f(x)=x2-4x,及f(-x)=-f(x)可得x<0时,函数的解析式,最后综合讨论结果,可得函数f(x)的解析式;
(3)分当x<0时和当x≥0时,两种情况求解方程f(x)=-5,最后综合讨论结果,可得答案.
(2)当x<0时,-x>0,结合x≥0,f(x)=x2-4x,及f(-x)=-f(x)可得x<0时,函数的解析式,最后综合讨论结果,可得函数f(x)的解析式;
(3)分当x<0时和当x≥0时,两种情况求解方程f(x)=-5,最后综合讨论结果,可得答案.
解答:
解 (1)∵当x≥0时,f(x)=x2-4x,
又由奇函数f(x)的图象关于原点对称,
故函数f(x)的图象如下图所示:
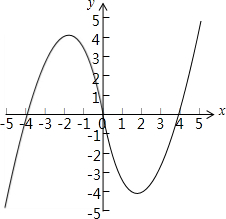 (4分)
(4分)
(2)∵当x≥0时,f(x)=x2-4x,
∴当x<0时,-x>0,
f(-x)=x2+4x=-f(x).
∴f(x)=-x2-4x,
∴f(x)=
(8分)
(3)当x≥0时,f(x)=x2-4x=-5无解;
当x<0时,解-x2-4x=-5得:x=-5,或x=1(舍去),
综上所述,满足方程f(x)=-5的解为:x=-5(12分)
又由奇函数f(x)的图象关于原点对称,
故函数f(x)的图象如下图所示:
 (4分)
(4分) (2)∵当x≥0时,f(x)=x2-4x,
∴当x<0时,-x>0,
f(-x)=x2+4x=-f(x).
∴f(x)=-x2-4x,
∴f(x)=
|
(3)当x≥0时,f(x)=x2-4x=-5无解;
当x<0时,解-x2-4x=-5得:x=-5,或x=1(舍去),
综上所述,满足方程f(x)=-5的解为:x=-5(12分)
点评:本题考查的知识点是函数奇偶生的性质,函数解析式的求法,熟练掌握函数奇偶性的性质是解答的关键.

练习册系列答案
相关题目
 如图,椭圆
如图,椭圆