题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{a,x=1}\\{(\frac{1}{2})^{|x-1|}+1,x≠1}\end{array}\right.$,若方程2f2(x)-(2a+3)f(x)+3a=0有5个不同的实数解,则a的范围是( )| A. | (1,$\frac{3}{2}$)∪($\frac{3}{2}$,2) | B. | (1,2)∪(2,3) | C. | (1,+∞) | D. | (1,3) |
分析 解方程可得f(x)=a或f(x)=$\frac{3}{2}$,讨论若a=$\frac{3}{2}$,可得原方程有3个不等实根;只要1+($\frac{1}{2}$)|x-1|=a有2个不等实根即可.运用指数函数的单调性,即可得到所求a的范围.
解答 解:方程2f2(x)-(2a+3)f(x)+3a=0,
解得f(x)=a或f(x)=$\frac{3}{2}$,
若a=$\frac{3}{2}$,f(x)=$\left\{\begin{array}{l}{a,x=1}\\{(\frac{1}{2})^{|x-1|}+1,x≠1}\end{array}\right.$,
可得x=1或0或2,不满足题意;
则a≠$\frac{3}{2}$,
由f(x)=$\frac{3}{2}$,可得原方程有3个不等实根;
只要1+($\frac{1}{2}$)|x-1|=a有2个不等实根即可.
由|x-1|>0可得0<($\frac{1}{2}$)|x-1|<1,
即有1<a<2,
综上可得a∈(1,$\frac{3}{2}$)∪($\frac{3}{2}$,2).
故选:A.
点评 本题考查方程的解的个数问题,注意运用分类讨论思想方法和转化思想,考查指数函数的性质,以及运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若tanα=3,tan(α+β)=2,则tanβ=( )
| A. | $-\frac{1}{7}$ | B. | $-\frac{1}{6}$ | C. | $-\frac{5}{7}$ | D. | $-\frac{5}{6}$ |
7.已知a≥2,f(x)=x3+3|x-a|,若函数f(x)在[-1,1]上的最大值和最小值分别记为M,m,则M-m的值为( )
| A. | 8 | B. | -a3-3a+4 | C. | 4 | D. | -a3+3a+2 |
4.设向量$\overrightarrow{a}$=(cosα,$\frac{\sqrt{2}}{2}$)的模为$\frac{\sqrt{3}}{2}$,则cos2α=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
11.某几何体的三视图如图所示,则该几何体的体积是( )
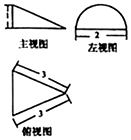

| A. | $\frac{{\sqrt{2}}}{3}π$ | B. | $\frac{π}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}π$ | D. | π |
8.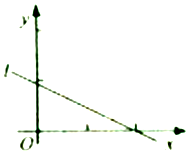 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是( )| A. | x和y的相关系数在-1和0之间 | |
| B. | x和y的相关系数为直线l的斜率 | |
| C. | 当n为偶数时,分布在l两侧的样本点的个数一定相同 | |
| D. | 所有样本点(xi,yi)(i=1,2,…,n)都在直线l上 |