题目内容
10．从编号为001，002，…，500的500个产品中用系统抽样的方法抽取一个样本，已知样本中编号最小的两个编号分别为007，032，则样本中最大的编号应该为482．分析 根据系统抽样的定义得到，编号之间的关系，即可得到结论．
解答 解：∵样本中编号最小的两个编号分别为007，032，
∴样本数据组距为32-7=25，则样本容量为$\frac{500}{25}$=20，
则对应的号码数x=7+25（n-1），当n=20时，x取得最大值为x=7+25×19=482，
故答案为：482．
点评 本题主要考查系统抽样的应用，根据条件确定组距是解决本题的关键，比较基础．
练习册系列答案
相关题目
20．要得到函数y=sin（2x-$\frac{π}{4}$）的图象，只要将函数y=sin2x的图象（ ）
| A． | 向左平移$\frac{π}{4}$ | B． | 向右平移$\frac{π}{4}$ | C． | 向左平移$\frac{π}{8}$ | D． | 向右平移$\frac{π}{8}$ |
1．已知定义在R上的可导函数f（x）的导函数为f′（x），若对于任意实数x，有f（x）＞f′（x），且f（0）=1，则不等式f（x）＜ex的解集为（ ）
| A． | （-∞，0） | B． | （0，+∞） | C． | （-∞，e4） | D． | （e4，+∞） |
18．已知向量$\overrightarrow{a}$=（cos5°，sin5°），$\vec b=（{cos65°，sin65°}）$，则$|{\vec a+2\vec b}|$=（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{7}$ |
2．将3颗骰子各掷一次，记事件A为“三个点数都不同”，事件B为“至少出现一个1点”，则条件概率P（A|B）和P（B|A）分别为（ ）
| A． | $\frac{1}{2}，\frac{60}{91}$ | B． | $\frac{5}{18}，\frac{60}{91}$ | C． | $\frac{60}{91}，\frac{1}{2}$ | D． | $\frac{91}{216}，\frac{1}{2}$ |
19．已知函数f（x）=$\left\{\begin{array}{l}{a，x=1}\\{（\frac{1}{2}）^{|x-1|}+1，x≠1}\end{array}\right.$，若方程2f2（x）-（2a+3）f（x）+3a=0有5个不同的实数解，则a的范围是（ ）
| A． | （1，$\frac{3}{2}$）∪（$\frac{3}{2}$，2） | B． | （1，2）∪（2，3） | C． | （1，+∞） | D． | （1，3） |
20．执行如图所示的程序框图，若输出的n=4，则输入整数p的最大值是（ ）
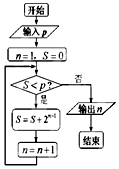
| A． | 4 | B． | 7 | C． | 8 | D． | 15 |