题目内容
已知大于1的正数x,y,z满足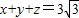 .
.(1)求证:
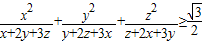 .
.(2)求
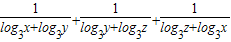 的最小值.
的最小值.
【答案】分析:(1)可以将不等式左边乘以)[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]然后利用柯西不等式进行放缩求解;
(2)根据对数函数的性质,然后再利用柯西不等式进行放缩,注意不等式取等号的条件进行证明;
解答:解:(1)由柯西不等式得,
( )[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]≥(x+y+z)2=27
)[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]≥(x+y+z)2=27
得: ;
;
(2)∵ =
= +
+ +
+ ,
,
由柯西不等式得:( +
+ +
+ )(log3(xy)+log3(yz)+log3(zx)),
)(log3(xy)+log3(yz)+log3(zx)),
由柯西不等式得:( +
+ +
+ )(log3(xy)+log3(yz)+log3(zx))≥9
)(log3(xy)+log3(yz)+log3(zx))≥9
所以, ,
,
 .
.
∴ .
.
∴ .得
.得
所以, 当且仅当
当且仅当 时,等号成立.
时,等号成立.
故所求的最小值是3.
点评:此题主要考查柯西不等式的应用,充分利用好条件 ,进行拆分,是解题的关键,此题是一道中档题;
,进行拆分,是解题的关键,此题是一道中档题;
(2)根据对数函数的性质,然后再利用柯西不等式进行放缩,注意不等式取等号的条件进行证明;
解答:解:(1)由柯西不等式得,
(
 )[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]≥(x+y+z)2=27
)[(x+2y+3z)+(y+2z+3x)+(z+2x+3y)]≥(x+y+z)2=27得:
 ;
;(2)∵
 =
= +
+ +
+ ,
,由柯西不等式得:(
 +
+ +
+ )(log3(xy)+log3(yz)+log3(zx)),
)(log3(xy)+log3(yz)+log3(zx)),由柯西不等式得:(
 +
+ +
+ )(log3(xy)+log3(yz)+log3(zx))≥9
)(log3(xy)+log3(yz)+log3(zx))≥9所以,
 ,
, .
.∴
 .
.∴
 .得
.得
所以,
 当且仅当
当且仅当 时,等号成立.
时,等号成立.故所求的最小值是3.
点评:此题主要考查柯西不等式的应用,充分利用好条件
 ,进行拆分,是解题的关键,此题是一道中档题;
,进行拆分,是解题的关键,此题是一道中档题; 
练习册系列答案
相关题目
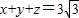 .
.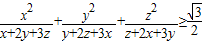 .
.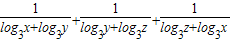 的最小值.
的最小值. .
. .
. 的最小值.
的最小值.