题目内容
已知大于1的正数x，y，z满足x+y+z=3
．
（1）求证：
+
+
≥
．
（2）求
+
+
的最小值．
| 3 |
（1）求证：
| x2 |
| x+2y+3z |
| y2 |
| y+2z+3x |
| z2 |
| z+2x+3y |
| ||
| 2 |
（2）求
| 1 |
| log3x+log3y |
| 1 |
| log3y+log3z |
| 1 |
| log3z+log3x |
（1）由柯西不等式得，
（
+
+
）[（x+2y+3z）+（y+2z+3x）+（z+2x+3y）]≥（x+y+z）2=27
得：
+
+
≥
；
（2）∵
+
+
=
+
+
，
由柯西不等式得：（
+
+
）（log3（xy）+log3（yz）+log3（zx）），
由柯西不等式得：（
+
+
）（log3（xy）+log3（yz）+log3（zx））≥9
所以，(
+
+
)≥
=
，
又∵3
=x+y+z≥3
．
∴xyz≤3
．
∴log3xyz≤
．得
≥
×
=3
所以，
+
+
≥3当且仅当x=y=z=
时，等号成立．
故所求的最小值是3．
（
| x2 |
| x+2y+3z |
| y2 |
| y+2z+3z |
| z2 |
| z+2x+3y |
得：
| x2 |
| x+2y+3z |
| y2 |
| y+2z+3x |
| z2 |
| z+2x+3y |
| ||
| 2 |
（2）∵
| 1 |
| log3x+log3y |
| 1 |
| log3y+log3z |
| 1 |
| log3z+log3x |
| 1 |
| log3(xy) |
| 1 |
| log3(yz) |
| 1 |
| log3(zx) |
由柯西不等式得：（
| 1 |
| log3(xy) |
| 1 |
| log3(yz) |
| 1 |
| log3(zx) |
由柯西不等式得：（
| 1 |
| log3(xy) |
| 1 |
| log3(yz) |
| 1 |
| log3(zx) |
所以，(
| 1 |
| log3(xy) |
| 1 |
| log3(yz) |
| 1 |
| log3(zx) |
| 9 |
| (log3(xy)+log3(yz)+log3(zx)) |
| 9 |
| 2log3(xyz) |
又∵3
| 3 |
| 3 | xyz |
∴xyz≤3
| 3 |
∴log3xyz≤
| 3 |
| 2 |
| 9 |
| 2log3xyz |
| 9 |
| 2 |
| 2 |
| 3 |
所以，
| 1 |
| log3x+log3y |
| 1 |
| log3y+log3z |
| 1 |
| log3z+log3x |
| 3 |
故所求的最小值是3．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
．
．
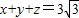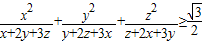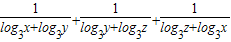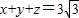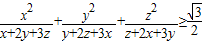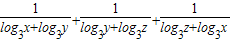的最小值．
．
．
的最小值．
．
．
的最小值．