题目内容
如图,
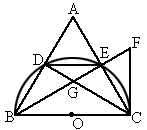
BC是半圆的直径,D、E是半圆上的两点,且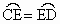 .过C作半圆的切线,与BE的延长线相交于F,BE与CD相交于G,CE、BD的延长线相交于A,连结DE.
.过C作半圆的切线,与BE的延长线相交于F,BE与CD相交于G,CE、BD的延长线相交于A,连结DE.
(1)
求证:AB=BC;(2)
如果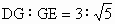 ,BG=3k,试用含k的代数式表示AC;
,BG=3k,试用含k的代数式表示AC;
(3)
设FC=a,BF+FC=b,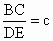 ,求证:
,求证: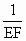 是方程
是方程 的根,并求出这个方程的另一个根.
的根,并求出这个方程的另一个根.
答案:略
解析:
提示:
解析:
|
(1) 证明: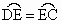 ,∴∠ABE=∠CBE. ,∴∠ABE=∠CBE.
∵BC 是半圆的直径,∴∠AEB=∠CEB=90°.又 ∵BE=BE,∴△ABE≌△CBE.∴AB=BC .(2) 解:∵BC是半圆的直径,∴∠GEC=∠FEC=90 °.∵CF 是切线,∴∠GCE=∠CBE=∠FCE.又 ∵CF=CE,∴△CEG≌△CEF.∴CG=GF,EF=EG.由相交弦定理可得: 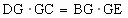 ,∴ ,∴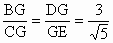 . .
由 BG=3k,得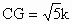 ,∴ ,∴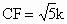 . .
∵CF 是半圆的切线,由切割线定理得,∴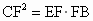 . .
设 EF=EG=x,则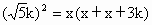 . .
解得 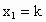 , ,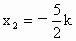 (舍去). (舍去).
∴EF=k .∴ . .
(3) 解:易证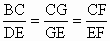 ,把 ,把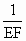 代入方程, 代入方程,
∴ 左边=右边.∴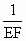 是方程 是方程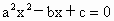 的根. 的根.
设另一根为 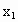 ,由韦达定理,得 ,由韦达定理,得
∴ 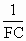  . . |
提示:

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
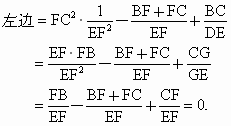
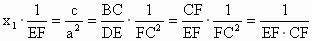
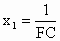
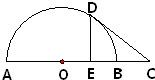 如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,则BC的长为
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,则BC的长为 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)