Question

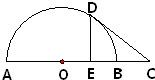如图，AB是半圆的直径，C是AB延长线上一点，CD切半圆于点D，CD=2，DE⊥AB，垂足为E，且E是OB的中点，则BC的长为

 

．

Answer 1

分析：连接OD、BD，由题目中条件：“DE⊥AB，垂足为E，且E是OB的中点”可得三角形BOD是等边三角形，再在直角三角形OCD中，可得OD的长，最后根据题中圆的切线条件再依据切割线定理求得BC的长．

解答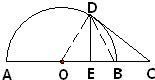：解：连接OD、BD，
∵DE⊥AB，垂足为E，且E是OB的中点
∴可得等腰三角形BOD是等边三角形，
∵在直角三角形OCD中，CD=2，
∴可得OD=

2 3

3

，
∵CD是圆O的切线，∴由切割线定理得，
∴CD²=CB×CA，
即4=CB×（CB+

4 3

3

）
∴BC=

2

3

3

，
故填：

2

3

3

．

点评：此题综合运用了切割线定理、切线的性质定理，本题主要考查与圆有关的比例线段、圆中的切割线定理，属于基础题．