题目内容
△ABC中，∠A，∠B，∠C所对的边分别为a，b，c．若a=3，b=4，∠C=60°，则c的值等于
- A.5
- B.13
- C.
- D.
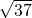
C
分析：由C的度数求出cosC的值，再由a与b的值，利用余弦定理列出关于c的方程，求出方程的解即可得到c的值．
解答：∵a=3，b=4，∠C=60°，
∴根据余弦定理得：c2=a2+b2-2ab•cosC=9+16-12=13，
则c=．
故选C
点评：此题考查了余弦定理，以及特殊角的三角函数值，余弦定理很好的建立了三角形的边角关系，熟练掌握余弦定理是解本题的关键．
分析：由C的度数求出cosC的值，再由a与b的值，利用余弦定理列出关于c的方程，求出方程的解即可得到c的值．
解答：∵a=3，b=4，∠C=60°，
∴根据余弦定理得：c2=a2+b2-2ab•cosC=9+16-12=13，
则c=
．故选C
点评：此题考查了余弦定理，以及特殊角的三角函数值，余弦定理很好的建立了三角形的边角关系，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目