题目内容
已知函数 ,若同时满足条件:
,若同时满足条件:①?x∈(0,+∞),x为f(x)的一个极大值点;
②?x∈(8,+∞),f(x)>0.
则实数a的取值范围是( )
A.(4,8]
B.[8,+∞)
C.(-∞,0)∪[8,+∞)
D.(-∞,0)∪(4,8]
【答案】分析:求导数,由①得到 ;
;
由②?x∈(8,+∞),f(x)>0,故只需f(x)在(8,+∞)上的最小值大于0即可,
分别解出不等式即可得到实数a的取值范围为4<a≤8.
解答:解:由于 ,则
,则 =
=
令f′(x)=0,则 ,
,
故函数f(x)在(-∞,x1),(x2,+∞)上递增,在(x1,x2)上递减
由于?x∈(8,+∞),f(x)>0,故只需f(x)在(8,+∞)上的最小值大于0即可,
当x2>8,即 时,函数f(x)在(8,+∞)上的最小值为
时,函数f(x)在(8,+∞)上的最小值为 ,此时无解;
,此时无解;
当x2≤8,即 时,函数f(x)在(8,+∞)上的最小值为
时,函数f(x)在(8,+∞)上的最小值为 ,解得a≤8.
,解得a≤8.
又由?x∈(0,+∞),x为f(x)的一个极大值点,故 解得a>4;
解得a>4;
故实数a的取值范围为4<a≤8
故答案为 A
点评:本题考查函数在某点取得极值的条件,属于基础题.
 ;
;由②?x∈(8,+∞),f(x)>0,故只需f(x)在(8,+∞)上的最小值大于0即可,
分别解出不等式即可得到实数a的取值范围为4<a≤8.
解答:解:由于
 ,则
,则 =
=
令f′(x)=0,则
 ,
,
故函数f(x)在(-∞,x1),(x2,+∞)上递增,在(x1,x2)上递减
由于?x∈(8,+∞),f(x)>0,故只需f(x)在(8,+∞)上的最小值大于0即可,
当x2>8,即
 时,函数f(x)在(8,+∞)上的最小值为
时,函数f(x)在(8,+∞)上的最小值为 ,此时无解;
,此时无解;当x2≤8,即
 时,函数f(x)在(8,+∞)上的最小值为
时,函数f(x)在(8,+∞)上的最小值为 ,解得a≤8.
,解得a≤8.又由?x∈(0,+∞),x为f(x)的一个极大值点,故
 解得a>4;
解得a>4;故实数a的取值范围为4<a≤8
故答案为 A
点评:本题考查函数在某点取得极值的条件,属于基础题.

练习册系列答案
相关题目
已知函数![]() ,若同时满足条件:
,若同时满足条件:
①∃x0∈(0,+∞),x0为f(x)的一个极大值点;
②∀x∈(8,+∞),f(x)>0.
则实数a的取值范围是( )
|
| A. | (4,8] | B. | [8,+∞) | C. | (﹣∞,0)∪[8,+∞) | D. | (﹣∞,0)∪(4,8] |
已知函数![]() ,若同时满足条件:
,若同时满足条件:
①∃x0∈(0,+∞),x0为f(x)的一个极大值点;
②∀x∈(8,+∞),f(x)>0.
则实数a的取值范围是( )
|
| A. | (4,8] | B. | [8,+∞) | C. | (﹣∞,0)∪[8,+∞) | D. | (﹣∞,0)∪(4,8] |
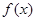 ,(
,(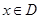 ),若同时满足以下条件:
),若同时满足以下条件: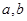 ]
]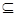 D,使
D,使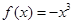 符合条件②的区间[
符合条件②的区间[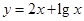 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[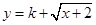 是闭函数,求实数
是闭函数,求实数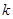 的取值范围.
的取值范围. ,若同时满足条件:
,若同时满足条件: