题目内容
18.已知△ABC的内角A,B,C所对的边分别为a,b,c,且a,b,c成等比数列,cosB=$\frac{3}{5}$.(Ⅰ)求$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$的值;
(Ⅱ)若△ABC的面积为2,求△ABC的周长.
分析 (Ⅰ)根据cosB求出sinB的值,利用a,b,c成等比数列,根据正弦定理和同角三角函数的基本关系及诱导公式,求出$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$的值;
(Ⅱ)根据△ABC的面积公式求出b的值,再利用余弦定理求出a2+c2以及a+c即可.
解答 解:(Ⅰ)△ABC中,∵cosB=$\frac{3}{5}$>0,
∴sinB=$\sqrt{1{-cos}^{2}B}$=$\frac{4}{5}$,
由a,b,c成等比数列,得b2=ac,
根据正弦定理得:sin2B=sinAsinC,
∴$\frac{cosA}{sinA}$+$\frac{cosC}{sinC}$=$\frac{cosAsinC+sinAcosC}{sinAsinC}$
=$\frac{sin(A+C)}{sinAsinC}$
=$\frac{sin(π-B)}{sinAsinC}$
=$\frac{sinB}{sinAsinC}$
=$\frac{sinB}{{sin}^{2}B}$
=$\frac{1}{sinB}$
=$\frac{5}{4}$;
(Ⅱ)△ABC的面积为S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$b2•$\frac{4}{5}$=2,
∴b=$\sqrt{5}$;
由余弦定理b2=a2+c2-2accosB=a2+c2-2×5×$\frac{3}{5}$,
∴a2+c2=b2+6=5+5=11,
∴(a+c)2=a2+2ac+c2=11+2×5=21,
∴a+c=$\sqrt{21}$;
∴△ABC的周长为a+b+c=$\sqrt{21}$+$\sqrt{5}$.
点评 本题考查了正弦定理以及等比数列的性质和同角三角函数间的基本关系应用问题,是综合性题目.

 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 170石 | B. | 180石 | C. | 190石 | D. | 200石 |
| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | 4 |
| A. | $\frac{1}{n}>\frac{1}{m}$ | B. | |n|>|m| | C. | $\frac{n}{m}+\frac{m}{n}>2$ | D. | m+n>mn |
| 对篮球运动不感兴趣 | 对篮球运动感兴趣 | 总计 | |
| 男生 | 20 | 50 | 70 |
| 女生 | 10 | 40 | 50 |
| 总计 | 30 | 90 | 120 |
(2)采用分层抽样的方法从“对篮球运动不感兴趣”的学生里抽取一个6人的样本,其中男生和女生个多少人?从6人中随机选取3人做进一步的调查,求选取的3人中至少有1名女生的概率
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 5.635 | 7.879 | 10.828 |
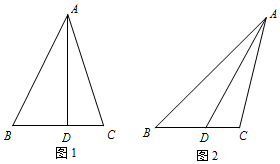 如图,在△ABC中,D为边BC上一点,AD=6,BD=3,
如图,在△ABC中,D为边BC上一点,AD=6,BD=3,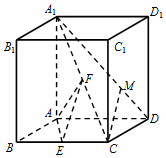 如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=$\frac{π}{3}$,E,F分别是BC,A1C的中点.