题目内容
与直线x+y-2=0和曲线x2+y2-12x-12y+54=0都相切的半径最小的圆的标准方程是 ．
【答案】分析：由题意可知先求圆心坐标，再求圆心到直线的距离，求出最小的圆的半径，圆心坐标，可得圆的方程．
解答：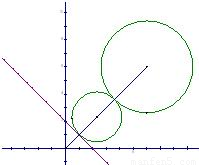
解：曲线化为（x-6）2+（y-6）2=18，
其圆心到直线x+y-2=0的距离为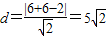
．
所求的最小圆的圆心在直线y=x上，
其到直线的距离为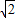
，圆心坐标为（2，2）．
标准方程为（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
点评：本题考查直线和圆的方程的应用，考查转化的数学思想，是中档题．
解答：
解：曲线化为（x-6）2+（y-6）2=18，其圆心到直线x+y-2=0的距离为
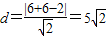．所求的最小圆的圆心在直线y=x上，
其到直线的距离为
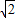，圆心坐标为（2，2）．标准方程为（x-2）2+（y-2）2=2．
故答案为：（x-2）2+（y-2）2=2．
点评：本题考查直线和圆的方程的应用，考查转化的数学思想，是中档题．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
（2012•南京二模）如图，在平面直角坐标系xOy中，椭圆C：