题目内容
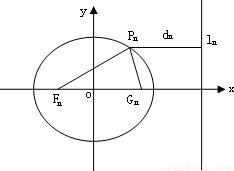
已知一列椭圆Cn:x2+![]() =1. 0<bn<1,n=1,2.
=1. 0<bn<1,n=1,2.![]() .若椭圆C上有一点Pn使Pn到右准线
.若椭圆C上有一点Pn使Pn到右准线![]() n的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
n的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
 (Ⅰ)试证:bn≤
(Ⅰ)试证:bn≤![]() (n≥1);
(n≥1);
(Ⅱ)取bn=![]() ,并用SA表示
,并用SA表示![]() PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
证:(1)由题设及椭圆的几何性质有
![]()
设![]()
![]()
因此,由题意![]() 应满足
应满足
![]()
即
即![]() ,
,
从而对任意![]()
(Ⅱ)设点![]()
![]()
![]()
得两极![]() ,从而易知f(c)在(
,从而易知f(c)在(![]() ,
,![]() )内是增函数,而在(
)内是增函数,而在(![]() ,1)内是减函数.
,1)内是减函数.
现在由题设取![]() 是增数列.又易知
是增数列.又易知
![]()
![]()
故由前已证,知![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
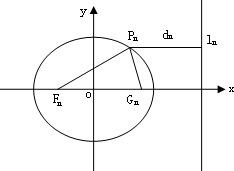 已知一列椭圆
已知一列椭圆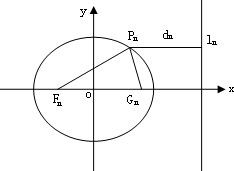 已知一列椭圆
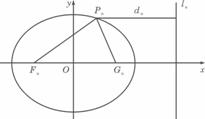
已知一列椭圆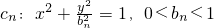 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.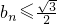 (n≥1);
(n≥1);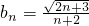 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).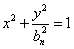 , 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,
, 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,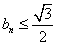 (n≥1);
(n≥1);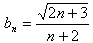 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。 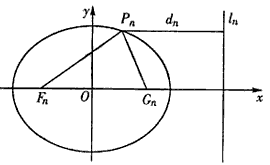
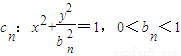 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点. (n≥1);
(n≥1);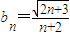 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).