题目内容
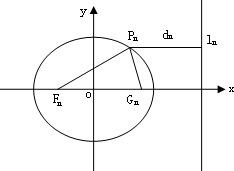 已知一列椭圆cn:x2+
已知一列椭圆cn:x2+| y2 | ||
|
(I)试证:bn≤
| ||
| 2 |
(II)取bn=
| ||
| n+2 |
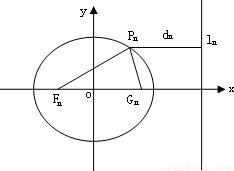
分析:(I)由题设及椭圆的几何性质有2dn={PnFn}+{PnGn}=2,故dn=4.设Gn=
,则右准线方程为ln2x=
.由题设条件能推出
≤Gn<1.即
≤
<1.从而证出对任意n≥1.bn≤
(II)设点P的坐标为(xn,yn),由题设条件能够推出{FnGn}=2Gn,△PnFnGn的面积为Sn=Gn{y4},由此入手能够证出S1<S2,且Sn>Sn+1(n≥3).
| 1-b2 |
| 1 |
| Gn |
| 1 |
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
(II)设点P的坐标为(xn,yn),由题设条件能够推出{FnGn}=2Gn,△PnFnGn的面积为Sn=Gn{y4},由此入手能够证出S1<S2,且Sn>Sn+1(n≥3).
解答:证明:(I)由题设及椭圆的几何性质有:
2dn={PnFn}+{PnGn}=2,故dn=1.
设Gn=
,则右准线方程为x=
.
因此,由题意dn应满足
-1≤dn≤
+1.
即
,解之得:
≤Gn<1.
即
≤
<1.从而对任意n≥1.bn≤
.
(II)设点P的坐标为(xn,yn),则由dn=1及椭圆方程易知xn=
-1,
=
(1-
)=(1-
)(1-(
-1)2)
=
(-2
+
+2Gn-1).因{FnGn}=2Gn,
故△PnFnGn的面积为Sn=Gn{y4},
从而
=-2
+
+2Gn-1(
<Gn<1).
令f(c)=-2c3+c2+2c-1.由f′(c)=-6c2+2c+2=0.
得两根
.从而易知函数f(c)在(
,
)内是增函数.
而在(
,1)内是减函数.
现在由题设取bn=
,
则Cn=
=
=1-
,Cn是增数列.
又易知C2=
<
<
=C3.
故由前已证,知S1<S2,且Sn>Sn+1(n≥3)
2dn={PnFn}+{PnGn}=2,故dn=1.
设Gn=
| 1-b2 |
| 1 |
| Gn |
因此,由题意dn应满足
| 1 |
| Gn |
| 1 |
| Gn |
即
|
| 1 |
| 2 |
即
| 1 |
| 2 |
1-
|
| ||
| 2 |
(II)设点P的坐标为(xn,yn),则由dn=1及椭圆方程易知xn=
| 1 |
| Gn |
| y | 2 n |
| b | 2 n |
| x | 2 n |
| G | 2 n |
| 1 |
| Gn |
=
| 1 | ||
|
| G | 2 n |
| G | 2 n |
故△PnFnGn的面积为Sn=Gn{y4},
从而
| S | 2 n |
| G | 3 n |
| G | 3 n |
| 1 |
| 2 |
令f(c)=-2c3+c2+2c-1.由f′(c)=-6c2+2c+2=0.
得两根
1±
| ||
| 6 |
| 1 |
| 2 |
1+
| ||
| 6 |
而在(
1+
| ||
| 6 |
现在由题设取bn=
| ||
| n+2 |
则Cn=
1-
|
| n+1 |
| n+2 |
| 1 |
| n+2 |
又易知C2=
| 3 |
| 4 |
1+
| ||
| 6 |
| 4 |
| 5 |
故由前已证,知S1<S2,且Sn>Sn+1(n≥3)
点评:本题综合考查椭圆、数列和不等式的知识,难度较大,解题时要综合考虑,恰当地选取公式.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
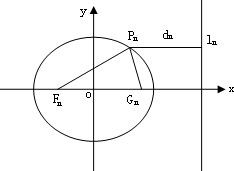 已知一列椭圆
已知一列椭圆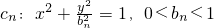 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.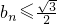 (n≥1);
(n≥1);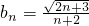 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
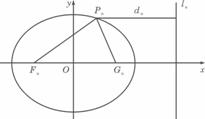
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).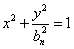 , 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,
, 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,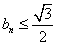 (n≥1);
(n≥1);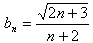 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。 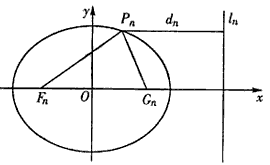
 (Ⅰ)试证:bn≤
(Ⅰ)试证:bn≤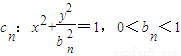 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点. (n≥1);
(n≥1);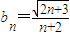 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).