题目内容
定义:若?x∈R,使得f(x)=x成立,则称x为函数y=f(x)的一个不动点(1)下列函数不存在不动点的是______(单选)
A.f(x)=1-logax(a>1)B.f(x)=x2+(b+2)x+1(b>1)C.f(x)=lnx D.f(x)=x
(2)设f(x)=2lnx-ax2(a∈R),求f(x)的极值
(3)设
 (e为自然对数的底数),当a>0时,讨论函数g(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.
(e为自然对数的底数),当a>0时,讨论函数g(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.
【答案】分析:(1)令x=1,可判断A中函数是否存在不动点,构造函数(x)=f(x)-x,判断函数是否存在零点,可判断B中函数是否存在不动点,根据不动点的定义,可判断D中函数有无数个不动点;
(2)求出函数的导函数,分析函数的单调性,进而可得函数的极值点,代入解析式可得函数的极值.
(3)若函数存在不动点,则方程g(x)=x有解,即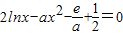 有解,利用导数法求出
有解,利用导数法求出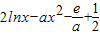 的最值,比较后可得结论.
的最值,比较后可得结论.
解答:解.(1)当x=1时,f(x)=1-logax=x,故A中函数f(x)存在不动点;
令g(x)=f(x)-x=x2+(b+1)x+1
∵b>1
∴△=(b+1)2-4>0
则方程g(x)=0有根,即B中函数f(x)存在不动点;
D中任意x值均为不动点,
故选C┅┅(4分)
(2)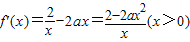
①当a=0时,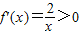 ,f(x)在(0,+∞)上位增函数,无极值;
,f(x)在(0,+∞)上位增函数,无极值;
②当a<0时,f'(x)>0恒成立,f(x)在(0,+∞)上位增函数,无极值;
③当a>0时,f'(x)=0,得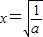 ,列表如下:
,列表如下:
当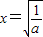 时,f(x)有极大值=
时,f(x)有极大值=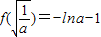
综上,当a≤0时无极值,当a>0时f(x)有极大值=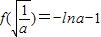 .┅┅(10分)
.┅┅(10分)
(3)假设存在不动点,则方程g(x)=x有解,即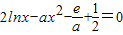 有解.
有解.
设h(x)=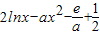 ,(a>0)有(2)可知h(x)极大值=
,(a>0)有(2)可知h(x)极大值=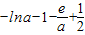 =
=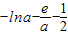 ,下面判断h(x)极大值是否大于0,设
,下面判断h(x)极大值是否大于0,设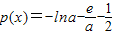 ,(a>0),
,(a>0), ,列表如下:
,列表如下:
当a=e时,p(a)极大值=p(e)=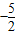 <0,所以
<0,所以 恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)
恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)
点评:本题考查的知识点是函数在某点取得极值的条件,函数的值,利用导数研究函数的单调性,导数是高考必考内容,其经典题型分析单调性,求极值,求最值一定要熟练掌握.
(2)求出函数的导函数,分析函数的单调性,进而可得函数的极值点,代入解析式可得函数的极值.
(3)若函数存在不动点,则方程g(x)=x有解,即
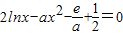 有解,利用导数法求出
有解,利用导数法求出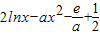 的最值,比较后可得结论.
的最值,比较后可得结论.解答:解.(1)当x=1时,f(x)=1-logax=x,故A中函数f(x)存在不动点;
令g(x)=f(x)-x=x2+(b+1)x+1
∵b>1
∴△=(b+1)2-4>0
则方程g(x)=0有根,即B中函数f(x)存在不动点;
D中任意x值均为不动点,
故选C┅┅(4分)
(2)
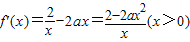
①当a=0时,
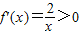 ,f(x)在(0,+∞)上位增函数,无极值;
,f(x)在(0,+∞)上位增函数,无极值;②当a<0时,f'(x)>0恒成立,f(x)在(0,+∞)上位增函数,无极值;
③当a>0时,f'(x)=0,得
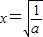 ,列表如下:
,列表如下:| X | 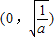 | 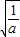 |  |
| f'(x) | + | _ | |
| f(x) | 增 | 极大值 | 减 |
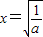 时,f(x)有极大值=
时,f(x)有极大值=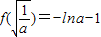
综上,当a≤0时无极值,当a>0时f(x)有极大值=
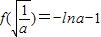 .┅┅(10分)
.┅┅(10分)(3)假设存在不动点,则方程g(x)=x有解,即
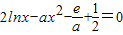 有解.
有解.设h(x)=
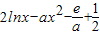 ,(a>0)有(2)可知h(x)极大值=
,(a>0)有(2)可知h(x)极大值=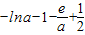 =
=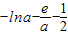 ,下面判断h(x)极大值是否大于0,设
,下面判断h(x)极大值是否大于0,设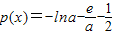 ,(a>0),
,(a>0), ,列表如下:
,列表如下:| A | (0,e)) | e | (e,+∞) |
| p'(a) | + | - | |
| P(a) | 增 | 极大值 | 减 |
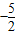 <0,所以
<0,所以 恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)
恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)点评:本题考查的知识点是函数在某点取得极值的条件,函数的值,利用导数研究函数的单调性,导数是高考必考内容,其经典题型分析单调性,求极值,求最值一定要熟练掌握.

练习册系列答案
相关题目
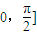 的函数f(x)=sinx,若
的函数f(x)=sinx,若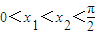 ,则必存在x∈(x1,x2),使(x1-x2)cosx=sinx1-sinx2成立;
,则必存在x∈(x1,x2),使(x1-x2)cosx=sinx1-sinx2成立; 成立的概率是
成立的概率是 ;
;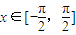 ,若f(x1)>f(x2),则不等式x12>x22必定成立.
,若f(x1)>f(x2),则不等式x12>x22必定成立.