题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点
(1)求sin 2α-tan α的值;
2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数y= -2f2(x)的最大值及对应的x的值.
-2f2(x)的最大值及对应的x的值.
解析:(1)因为角α终边经过点
所以 sin α=
sin α= ,cos α=-
,cos α=- ,tan α=-
,tan α=- ,
,
所以sin 2α-tan α=2sin αcos α-tan α
αcos α-tan α
=- +
+ =-
=- .
.
(2)因为f(x)=cos(x-α)cos α-sin(x-α)sin α=cos x,x∈R,
所以y= cos
cos -2cos2x=
-2cos2x= sin 2x-1-cos 2x=2si
sin 2x-1-cos 2x=2si n
n -1,
-1,
所以ymax=2-1=1,
此时sin =1,得2x-
=1,得2x- =2kπ+
=2kπ+ ,即x=kπ+
,即x=kπ+ (k∈Z).
(k∈Z).

练习册系列答案
相关题目
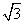 , 则直线AB的方程为 ( )
, 则直线AB的方程为 ( )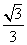 x+
x+ y=-
y=-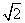 x+
x+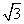 cos x(0≤x<2π)取得最大值时,x=________.
cos x(0≤x<2π)取得最大值时,x=________. +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1. ,则cos
,则cos 的值为( )
的值为( ) B.
B. C.±
C.± =( )
=( ) B.-
B.- C.
C. =________.
=________. (t为参数)的倾斜角为________.
(t为参数)的倾斜角为________.