题目内容
9.函数f(x)=|($\frac{1}{4}$)x-1|-2a有两个零点,则a的取值范围是( )| A. | (0,1) | B. | (0,1)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{1}{2}$) |
分析 函数f(x)=|($\frac{1}{4}$)x-1|-2a有两个零点,?函数y=|($\frac{1}{4}$)x-1|的图象与直线y=2a有两个交点点,
画出函数y=|($\frac{1}{4}$)x-1|的图象,根据图象可得a的取值范围.
解答 解:函数f(x)=|($\frac{1}{4}$)x-1|-2a有两个零点,?函数y=|($\frac{1}{4}$)x-1|的图象与直线y=2a有两个交点点,
函数y=|($\frac{1}{4}$)x-1|的图象如下:根据图象可得0<2a<1,⇒0<a<$\frac{1}{2}$
故选:D.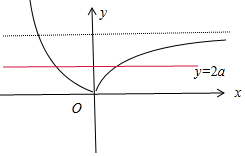
点评 本题考查的知识点是根的存在性及根的个数判断,数形结合思想,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键.属于中档题.

练习册系列答案
相关题目
10.已知非零向量$\overrightarrow{AB},\overrightarrow{AC}$满足$(\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|cosB}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|cosC}})•\overrightarrow{BC}=\overrightarrow{AB}•\overrightarrow{AC}$,则△ABC为( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
18.已知函数f(x)=x2+2x+a.若g(x)=$\frac{1}{{e}^{x}}$,对任意x1∈[$\frac{1}{2}$,2],存在x2∈[$\frac{1}{2}$,2],使f(x1)≤g(x2)成立,则实数a的取值范围是( )
| A. | (-∞,$\frac{\sqrt{e}}{e}$-8] | B. | [$\frac{\sqrt{e}}{e}$-8,+∞) | C. | [$\sqrt{2}$,e) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{e}{2}$] |
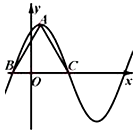 函数f(x)=6cos2$\frac{ωx}{2}$+2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+2$\sqrt{3}$sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.