题目内容
6.在△ABC中,若sin2A-sin2B-sin2C=sinBsinC,则∠A的大小为$\frac{2π}{3}$.分析 已知等式利用正弦定理化简,得到一个等式,再利用余弦定理列出关系式,将得出的等式代入求出cosA的值,即可确定出A的度数.
解答 解:已知等式利用正弦定理化简得:a2-b2-c2-bc=0,即b2+c2-a2=-bc,
∴由余弦定理得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,
∵∠A为三角形内角,
∴∠A=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 此题考查了正弦、余弦定理在解三角形中的应用,熟练掌握定理是解本题的关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知函数f(x)=10x-|lg(-x)|有两个零点x1,x2,则( )
| A. | $\frac{1}{10}$<x1x2<1 | B. | $\frac{1}{2}$<x1x2<1 | C. | $\frac{1}{e}$<x1x2<1 | D. | 1<x1x2<e |
15.在空间坐标系O-xyz中,已知点A(2,1,0),则与点A关于原点对称的点B的坐标为( )
| A. | (2,0,1) | B. | (-2,-1,0) | C. | (2,0,-1) | D. | (2,-1,0) |
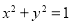 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线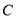 .
.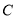 的参数方程;
的参数方程;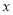 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线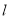 的极坐标方程为
的极坐标方程为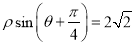 ,若
,若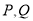 分别为曲线
分别为曲线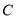 和直线
和直线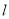 上的一点,求
上的一点,求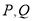 的最近距离.
的最近距离. (
( 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数 ( )
( )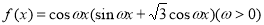 ,如果存在实数
,如果存在实数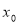 ,使得对任意的实数
,使得对任意的实数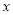 ,都有
,都有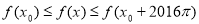 成立,则
成立,则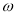 的最小值为( )
的最小值为( )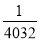 B.
B.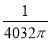 C.
C. D.
D.