题目内容
【题目】已知P为△ABC所在平面外一点,PA⊥PB,PB⊥PC,PC⊥PA,PH⊥平面 ABC,H,则H为△ABC的( ) 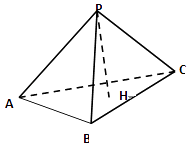
A.重心
B.垂心
C.外心
D.内心
【答案】B
【解析】证明:连结AH并延长,交BC与D连结BH并延长,交AC与E;
因PA⊥PB,PA⊥PC,故PA⊥面PBC,故PA⊥BC;
因PH⊥面ABC,故PH⊥BC,故BC⊥面PAH,
故AH⊥BC即AD⊥BC;
同理:BE⊥AC;
故H是△ABC的垂心.
故选:B
【考点精析】利用空间中直线与直线之间的位置关系和直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;垂直于同一个平面的两条直线平行.

练习册系列答案
相关题目