题目内容
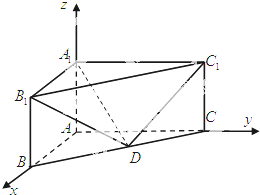三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中，已知AB=2，AC=4，AA1=3．D是BC的中点．（1）求直线A1D与B1C1所成角的余弦值；
（2）求直线DB1与平面A1C1D所成角的正弦值．
分析：（1）根据题中所给的坐标系，可得A、B、C、D、A1、B1、C1各点的坐标，由此得到向量
、
、
、
、
的坐标，利用空间向量的夹角公式算出cos＜
，
＞的值，即可得到直线A1D与B1C1所成角的余弦值；
（2）设平面A1C1D的一个法向量为
=（x，y，z），利用垂直向量数量积为零的方法建立方程组，解出
=（3，0，1），从而得到直线DB1与平面A1C1D所成角θ满足sinθ=cos＜
，
＞=
，即得直线DB1与平面A1C1D所成角的正弦值．
| A1D |
| A1C1 |
| DB |
| B 1C1 |
| DB1 |
| A1D |
| B 1C1 |
（2）设平面A1C1D的一个法向量为
| n |
| n |
| DB1 |
| n |
3
| ||
| 35 |
解答：解：根据题意，得A（0，0，0），B（2，0，0），C（0，4，0），D（1，2，0），
A1（0，0，3），B1（2，0，3），C1（0，4，3），
由此可得
=（1，2，-3），
=（0，4，0），
=（1，-2，0），
=（-2，4，0），
=（1，-2，3）
（1）∵cos＜
，
＞=
=
，
∴直线A1D与B1C1所成角的余弦值为
；
（2）设平面A1C1D的一个法向量为
=（x，y，z），
则
，取z=1得x=3，y=0，
∴
=（3，0，1）是平面A1C1D的一个法向量
因此，设直线DB1与平面A1C1D所成角为θ，
可得sinθ=cos＜
，
＞=
=
，
即直线DB1与平面A1C1D所成角的正弦值等于
．
A1（0，0，3），B1（2，0，3），C1（0，4，3），
由此可得
| A1D |
| A1C1 |
| DB |
| B 1C1 |
| DB1 |
（1）∵cos＜
| A1D |
| B 1C1 |
| -2+8 | ||||
|
3
| ||
| 70 |
∴直线A1D与B1C1所成角的余弦值为
3
| ||
| 70 |
（2）设平面A1C1D的一个法向量为
| n |
则
|
∴
| n |
因此，设直线DB1与平面A1C1D所成角为θ，
可得sinθ=cos＜
| DB1 |
| n |
| 3+3 | ||||
|
3
| ||
| 35 |
即直线DB1与平面A1C1D所成角的正弦值等于
3
| ||
| 35 |
点评：本题给出底面为直角三角形的直三棱柱，求异面直线所成角和直线与平面所成角的正弦值，着重考查了利用空间坐标系求空间直线与平面所成角和异面直线所成角等知识点，属于中档题．
练习册系列答案
相关题目
在三棱柱ABC-A1B1C1中，侧面AA1B1B是边长为2的正方形，点C在平面AA1B1B上的射影H恰好为A1B的中点，且CH=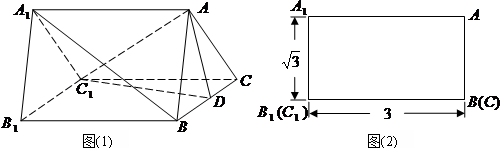
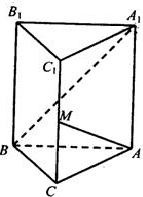如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，
如图：在直三棱柱ABC-A1B1C1中，已知AB=A1A，AC=BC，点D、E分别为C1C、AB的中点，O为A1B与AB1的交点．