题目内容
【题目】设等差数列{an}的前项和为Sn , 且a2=2,S5=15,数列{bn}的前项和为Tn , 且b1= ![]() ,2nbn+1=(n+1)bn(n∈N*)
,2nbn+1=(n+1)bn(n∈N*)
(Ⅰ)求数列{an}通项公式an及前项和Sn;
(Ⅱ) 求数列{bn}通项公式bn及前项和Tn .
【答案】解:(Ⅰ)由等差数列{an}的公差为d,由等差数列的性质可知:S5=5a3=15,则a3=3,
d=a3﹣a2=1,
首项a1=1,
∴数列{an}通项公式an=1+(n﹣1)=n,
前n项和Sn= ![]() =
= ![]() ;
;
(Ⅱ)2nbn+1=(n+1)bn(n∈N*),
则 ![]() =
= ![]()
![]() .,
.,
∴ ![]() =
= ![]()
![]() ,
, ![]() =
= ![]()
![]() ,
, ![]() =
= ![]() ×
× ![]() ,…
,… ![]() =
= ![]()
![]() ,
,
∴当n≥2时, ![]() =(
=( ![]() )n﹣1 , 即bn=
)n﹣1 , 即bn= ![]() ,
,
当n=1时,b1= ![]() ,符合上式,
,符合上式,
∴数列{bn}通项公式bn= ![]() ,
,
∴Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
两式相减得: ![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() ,
,
= ![]() ﹣
﹣ ![]() ,
,
=1﹣ ![]() ﹣
﹣ ![]() ,
,
=1﹣ ![]() ,
,
Tn=2﹣ ![]() ,
,
数列{bn}前项和Tn=2﹣ ![]() .
.
【解析】(Ⅰ)由等差数列的性质可知:S5=5a3=15,则a3=3,d=a3﹣a2=1,a1=1,根据等差数列通项公式及前n项和公式即可求得an及Sn;(Ⅱ)由题意可知: ![]() =
= ![]()
![]() ,采用累乘法即可求得数列{bn}通项公式bn=
,采用累乘法即可求得数列{bn}通项公式bn= ![]() ,利用错位相减法求得数列{bn}前项和Tn .
,利用错位相减法求得数列{bn}前项和Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系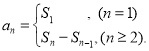 .
.

【题目】某公司生产![]() 、
、![]() 两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
两种产品,且产品的质量用质量指标来衡量,质量指标越大表明产品质量越好.现按质量指标划分:质量指标大于或等于82为一等品,质量指标小于82为二等品.现随机抽取这两种产品各100件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
产品 | 8 | 12 | 40 | 32 | 8 |
产品 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)请估计![]() 产品的一等奖;
产品的一等奖;
(Ⅱ)已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
已知每件![]() 产品的利润
产品的利润![]() (单位:元)与质量指标值
(单位:元)与质量指标值![]() 的关系式为:
的关系式为: 
(i)分别估计生产一件![]() 产品,一件
产品,一件![]() 产品的利润大于0的概率;
产品的利润大于0的概率;
(ii)请问生产![]() 产品,
产品, ![]() 产品各100件,哪一种产品的平均利润比较高.
产品各100件,哪一种产品的平均利润比较高.