Question

【题目】已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜ ）的部分图象如图所示．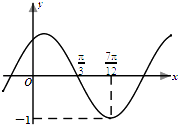
（1）求函数y=f（x）的解析式；
（2）求函数y=f（x）的单调增区间；
（3）求方程f（x）=0的解集．

Answer 1

【答案】
（1）解：由图知，A=1，

∵周期T=4（ ﹣ ）=π，

∴ω= =2，

∴f（x）=sin（2x+φ），

又f（ ）=﹣1，

∴sin（ +φ）=﹣1，

∴ +φ=2kπ+ （k∈Z），

∴φ=2kπ+ （k∈Z），又|φ|＜ ，

∴φ= ，

∴f（x）=sin（2x+ ）

（2）解：﹣ +2kπ≤2x+ ≤ +2kπ，k∈Z．

∴﹣ +kπ≤x≤ +kπ，k∈Z．

∴函数y=f（x）的单调增区间为：[﹣ +kπ， +kπ]k∈Z

（3）解：∵f（x）=0，

∴2x+ =kπ，k∈Z．

∴x=﹣ + kπ，k∈Z．

∴方程f（x）=0的解集为{x|x=﹣ + kπ，k∈Z}

【解析】（1）由图知，A=1，T=π，于是知ω=2；再由f（ ）=﹣1，可求得φ=2kπ+ （k∈Z），又|φ|＜ ，于是可得φ及函数y=f（x）的解析式；（2）利用正弦函数的单调性，由﹣ +2kπ≤2x+ ≤ +2kπ（k∈Z）可求函数y=f（x）的单调增区间；（3）f（x）=02x+ =kπ（k∈Z），从而可求得方程f（x）=0的解集．
【考点精析】本题主要考查了函数y=Asin（ωx+φ）的图象变换的相关知识点，需要掌握图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象才能正确解答此题．