题目内容
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
20 |
|
|
|
乙班 |
|
60 |
|
|
合计 |
|
|
210 |
(Ⅰ)请完成上面的 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求 的分布列及数学期望
的分布列及数学期望 .
.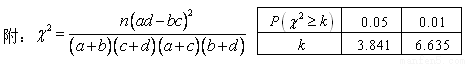
(Ⅰ)
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
20 |
90 |
110 |
|
乙班 |
40 |
60 |
100 |
|
合计 |
60 |
150 |
210 |
 所以按照99%的可靠性要求,能够判断成绩与班级有关。
所以按照99%的可靠性要求,能够判断成绩与班级有关。
(Ⅱ) 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
 。
。
【解析】
试题分析:(Ⅰ)
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
20 |
90 |
110 |
|
乙班 |
40 |
60 |
100 |
|
合计 |
60 |
150 |
210 |
 所以按照99%的可靠性要求,能够判断成绩与班级有关
6分
所以按照99%的可靠性要求,能够判断成绩与班级有关
6分
(Ⅱ) 且
且 ,
, 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
 12分
12分
考点:随机变量的分布列及其数学期望,卡方检验。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。解答本题的关键之一,是理解 本题对计算能力要求较高。
本题对计算能力要求较高。

有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下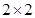 联表:
联表:
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
30 |
|
|
|
乙班 |
|
50 |
|
|
合计 |
|
|
200 |
已知全部200人中随机抽取1人为优秀的概率为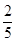
(1)请完成上面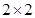 联表;
联表;
(2)根据列联表的数据,能否有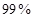 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为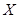 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求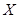 的分布列,期望
的分布列,期望 和方差
和方差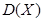
参考公式与参考数据如下:
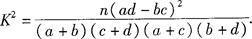
| 优秀 | 不优秀 | 合计 |
甲班 | 10 | 35 | 45 |
乙班 | 7 | 38 | 45 |
合计 | 17 | 73 | 90 |
利用列联表的独立性检验估计成绩与班级是否有关系.




