题目内容
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:已知从全部210人中随机抽取1人为优秀的概率为
.
(Ⅰ)请完成下面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.
附:x2=
| 2 |
| 7 |
(Ⅰ)请完成下面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望Eξ.
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 20 | ||
| 乙班 | 60 | ||
| 合计 | 210 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P=(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析:(I)假设H0:“成绩与班级无关”.由于从全部210人中随机抽取1人为优秀的概率为
,可得优秀的人数=210×
.即可得到乙班优秀的人数,甲班非优秀的人数,利用K2=
计算出K2与6.635比较即可得出结论.
(II)由题意可知:ξ~B(3,
),即可得出其分布列和数学期望.
| 2 |
| 7 |
| 2 |
| 7 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(II)由题意可知:ξ~B(3,
| 2 |
| 7 |
解答:解:(I)假设H0:“成绩与班级无关”.
∵从全部210人中随机抽取1人为优秀的概率为
,
∴优秀的人数=210×
=60.
∴乙班优秀的人数=60-20=40,
甲班非优秀的人数=210-60-60=90.
∴K2=
=12.218>6.635,
∴P(K2≥6.635)≈0.01.
因此假设不成立.
故认为“成绩与班级有关”;
(II)由题意可知:ξ~B(3,
).
∴P(ξ=i)=
(
)i(
)3-i(i=0,1,2,3).
∴Eξ=3×
=
.
∵从全部210人中随机抽取1人为优秀的概率为
| 2 |
| 7 |
∴优秀的人数=210×
| 2 |
| 7 |
∴乙班优秀的人数=60-20=40,
甲班非优秀的人数=210-60-60=90.
∴K2=
| 210×(20×60-40×90)2 |
| (20+90)×(40+60)×(20+40)×(90+60) |
∴P(K2≥6.635)≈0.01.
因此假设不成立.
故认为“成绩与班级有关”;
(II)由题意可知:ξ~B(3,
| 2 |
| 7 |
∴P(ξ=i)=
| C | i 3 |
| 2 |
| 7 |
| 5 |
| 7 |
∴Eξ=3×
| 2 |
| 7 |
| 6 |
| 7 |
点评:本题考查了独立性检验、二项分布列及其数学期望,属于中档题.

练习册系列答案
相关题目
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下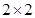 联表:
联表:
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
30 |
|
|
|
乙班 |
|
50 |
|
|
合计 |
|
|
200 |
已知全部200人中随机抽取1人为优秀的概率为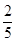
(1)请完成上面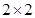 联表;
联表;
(2)根据列联表的数据,能否有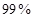 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为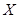 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求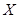 的分布列,期望
的分布列,期望 和方差
和方差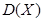
参考公式与参考数据如下:
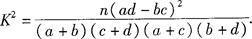
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
20 |
|
|
|
乙班 |
|
60 |
|
|
合计 |
|
|
210 |
(Ⅰ)请完成上面的 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(Ⅱ)从全部210人中有放回抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求 的分布列及数学期望
的分布列及数学期望 .
.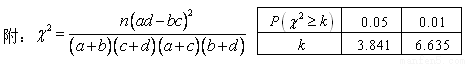
有甲、乙两个班级进行一门课的考试,按照学生的考试成绩优秀和不优秀统计成绩后,得到如下的列联表.
| 优秀 | 不优秀 | 合计 |
甲班 | 10 | 35 | 45 |
乙班 | 7 | 38 | 45 |
合计 | 17 | 73 | 90 |
利用列联表的独立性检验估计成绩与班级是否有关系.