题目内容
已知数列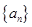 中,
中,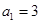 ,前
,前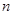 项和
项和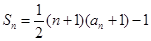 .
.
(1) 求数列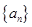 的通项公式;
的通项公式;
(2) 设数列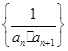 的前
的前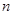 项和为
项和为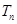 ,是否存在实数
,是否存在实数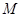 ,使得
,使得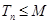 对一切正整数
对一切正整数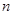 都
都
成立?若存在,求出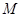 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
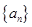 中,
中,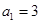 ,前
,前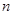 项和
项和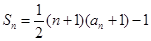 .
.(1) 求数列
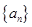 的通项公式;
的通项公式;(2) 设数列
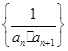 的前
的前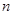 项和为
项和为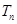 ,是否存在实数
,是否存在实数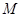 ,使得
,使得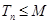 对一切正整数
对一切正整数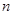 都
都成立?若存在,求出
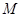 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:本题主要考查等差数列的证明、等差数列的通项公式、累加法、裂项相消法等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,将
 中的n用n+1代替得到新的表达式,两式子相减得到
中的n用n+1代替得到新的表达式,两式子相减得到 ,再将这个式子中的n用n+1代替,得到一个新的式子,两式子相减得到
,再将这个式子中的n用n+1代替,得到一个新的式子,两式子相减得到 ,从而证明了数列为等差数列;第二问,利用第一问的结论
,从而证明了数列为等差数列;第二问,利用第一问的结论 ,先计算通项
,先计算通项 ,通过裂项化简,利用裂项相消法求和,得到
,通过裂项化简,利用裂项相消法求和,得到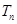 ,再放缩,与
,再放缩,与 作比较.
作比较.试题解析:(1)(解法一)∵
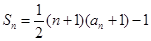
∴

∴

 3分
3分整理得

∴

两式相减得
 5分
5分即

∴
 ,即
,即 7分
7分∴ 数列
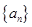 是等差数列
是等差数列且
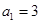 ,得
,得 ,则公差
,则公差
∴
 8分
8分(解法二) ∵
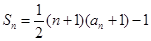
∴

∴

 3分
3分整理得

等式两边同时除以
 得
得  , 5分
, 5分即
 6分
6分累加得



得
 8分
8分(2) 由(1)知

∴

 10分
10分∴


 12分
12分则要使得
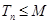 对一切正整数
对一切正整数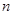 都成立,只要
都成立,只要 ,所以只要
,所以只要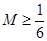
∴ 存在实数
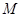 ,使得
,使得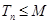 对一切正整数
对一切正整数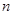 都成立,且
都成立,且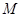 的最小值为
的最小值为 14分
14分
练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.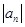 ,
,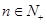 。
。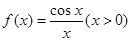 ,
,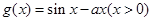 .
.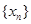 ,求
,求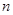 项和
项和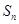 ;
; 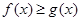 在
在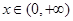 上恒成立,求实数
上恒成立,求实数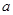 的取值范围;
的取值范围;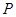 是函数
是函数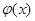 与
与 图象的交点,若直线
图象的交点,若直线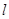 同时与函数
同时与函数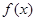 与
与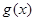 存在分切线?若存在,求出实数
存在分切线?若存在,求出实数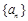 的首项
的首项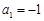 ,公差
,公差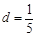 ,则
,则



 中,已知
中,已知 ,则
,则 .
.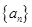 中,前n项和为
中,前n项和为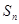 ,若
,若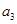 +
+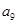 =6,则
=6,则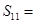 ( )
( )