题目内容
(本小题满分16分)
已知等差数列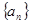 中,
中,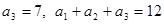 ,令
,令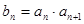 ,数列
,数列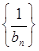 的前
的前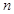 项和为
项和为 .
.
(1)求数列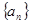 的通项公式;
的通项公式;
(2)求证: ;
;
(3)是否存在正整数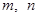 ,且
,且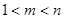 ,使得
,使得 ,
, ,
, 成等比数列?若存在,求出
成等比数列?若存在,求出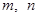 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知等差数列
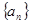 中,
中,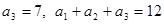 ,令
,令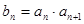 ,数列
,数列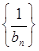 的前
的前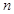 项和为
项和为 .
.(1)求数列
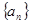 的通项公式;
的通项公式;(2)求证:
 ;
;(3)是否存在正整数
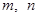 ,且
,且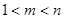 ,使得
,使得 ,
, ,
, 成等比数列?若存在,求出
成等比数列?若存在,求出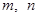 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)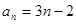 .(2)
.(2)
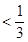 .
.
(3)不存在正整数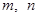 ,且
,且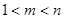 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.
综上,存在正整数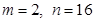 ,且
,且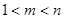 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)
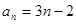 .(2)
.(2)
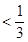 .
.(3)不存在正整数
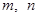 ,且
,且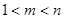 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.综上,存在正整数
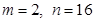 ,且
,且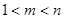 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)(1)由于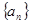 为等差数列,并且
为等差数列,并且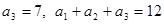 ,易求出
,易求出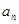 的通项公式,(2)在(1)的基础上可得
的通项公式,(2)在(1)的基础上可得 ,则
,则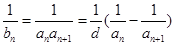 ,再采用裂项求和的方示求和.
,再采用裂项求和的方示求和.
(3)先假设 ,
, ,
, 成等比数列,则
成等比数列,则 ,即
,即 ,因为
,因为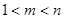 ,所以下面讨论按m=2,3,4,5,6,和
,所以下面讨论按m=2,3,4,5,6,和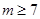 几种情况进行讨论求解.
几种情况进行讨论求解.
数学II(附加题)
(1)设数列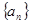 的公差为
的公差为 ,由
,由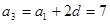 ,
, .
.
解得 ,
, ,∴
,∴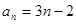 .(4分)
.(4分)
(2)∵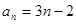 ,
, ,∴
,∴
∴
∴
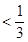 .(8分)
.(8分)
(3)由(2)知, ,∴
,∴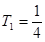 ,
, ,
, ,
,
∵
 ,
, ,
, 成等比数列,∴
成等比数列,∴ ,即
,即
当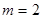 时,
时, ,
, ,符合题意;
,符合题意;
当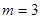 时,
时,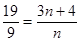 ,
,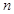 无正整数解;
无正整数解;
当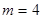 时,
时, ,
,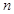 无正整数解;
无正整数解;
当 时,
时, ,
,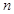 无正整数解;
无正整数解;
当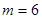 时,
时,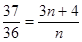 ,
,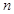 无正整数解;
无正整数解;
当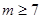 时,
时, ,则
,则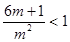 ,而
,而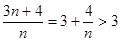 ,
,
所以,此时不存在正整数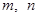 ,且
,且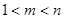 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.
综上,存在正整数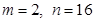 ,且
,且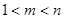 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)
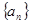 为等差数列,并且
为等差数列,并且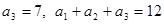 ,易求出
,易求出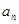 的通项公式,(2)在(1)的基础上可得
的通项公式,(2)在(1)的基础上可得 ,则
,则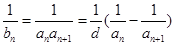 ,再采用裂项求和的方示求和.
,再采用裂项求和的方示求和.(3)先假设
 ,
, ,
, 成等比数列,则
成等比数列,则 ,即
,即 ,因为
,因为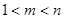 ,所以下面讨论按m=2,3,4,5,6,和
,所以下面讨论按m=2,3,4,5,6,和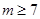 几种情况进行讨论求解.
几种情况进行讨论求解.数学II(附加题)
(1)设数列
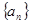 的公差为
的公差为 ,由
,由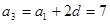 ,
, .
.解得
 ,
, ,∴
,∴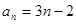 .(4分)
.(4分)(2)∵
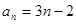 ,
, ,∴
,∴
∴

∴

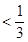 .(8分)
.(8分)(3)由(2)知,
 ,∴
,∴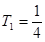 ,
, ,
, ,
,∵

 ,
, ,
, 成等比数列,∴
成等比数列,∴ ,即
,即
当
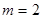 时,
时, ,
, ,符合题意;
,符合题意;当
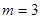 时,
时,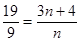 ,
,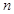 无正整数解;
无正整数解;当
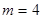 时,
时, ,
,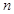 无正整数解;
无正整数解;当
 时,
时, ,
,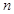 无正整数解;
无正整数解;当
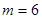 时,
时,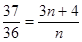 ,
,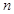 无正整数解;
无正整数解;当
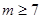 时,
时, ,则
,则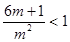 ,而
,而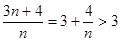 ,
,所以,此时不存在正整数
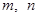 ,且
,且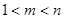 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.综上,存在正整数
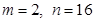 ,且
,且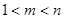 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)
练习册系列答案
相关题目
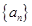 满足:
满足: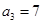 ,
,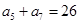 ,
,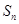 .
.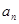 及
及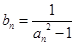 (
(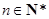 ),求数列
),求数列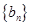 的前n项和
的前n项和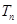 .
.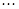
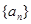 的各项均为正数,
的各项均为正数,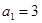 ,前n项和为
,前n项和为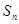 ,
,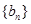 为等比数列,
为等比数列,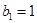 ,且
,且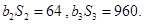
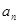 与
与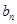 ;
;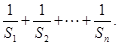
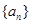 的各项均为正数,
的各项均为正数,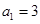 ,前
,前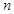 项和为
项和为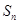 ,
,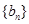 为等比数列,
为等比数列, 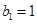 ,
,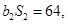
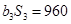 .
.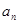 与
与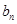 ;
;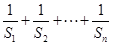 .
. 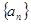 是公差不为0的等差数列,
是公差不为0的等差数列,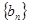 是等比数列,且
是等比数列,且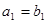 ,
,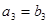 ,
,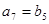 ,
,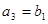
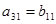
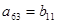
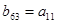
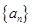 中,
中,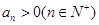 ,公比
,公比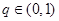 ,且
,且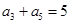 ,又
,又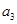 与
与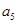 的等比中项为2.
的等比中项为2.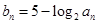 ,数列
,数列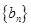 的前
的前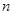 项和为
项和为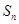 ,求数列
,求数列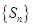 的通项公式;
的通项公式;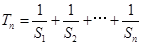 ,求
,求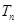 .
.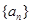 中,
中,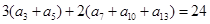 ,则此数列前13项的和为( )
,则此数列前13项的和为( )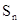 ,若
,若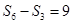 ,则
,则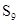 =____________.
=____________.