题目内容
(本小题满分12分)在等比数列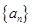 中,
中,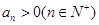 ,公比
,公比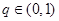 ,且
,且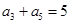 ,又
,又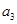 与
与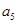 的等比中项为2.
的等比中项为2.
(1)求数列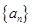 的通项公式;
的通项公式;
(2)设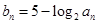 ,数列
,数列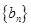 的前
的前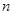 项和为
项和为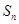 ,求数列
,求数列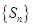 的通项公式;
的通项公式;
(3)设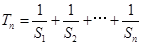 ,求
,求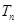 .
.
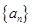 中,
中,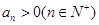 ,公比
,公比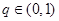 ,且
,且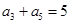 ,又
,又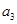 与
与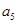 的等比中项为2.
的等比中项为2.(1)求数列
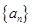 的通项公式;
的通项公式;(2)设
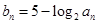 ,数列
,数列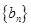 的前
的前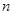 项和为
项和为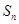 ,求数列
,求数列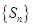 的通项公式;
的通项公式;(3)设
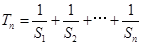 ,求
,求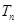 .
.(1) ;
;
(2) ,这就是数列
,这就是数列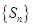 的通项公式。
的通项公式。
(3) 。
。
 ;
;(2)
 ,这就是数列
,这就是数列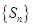 的通项公式。
的通项公式。(3)
 。
。本试题主要是考查了数列的通项公式的求解以及数列求和的综合运用。
(1)因为等比数列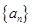 中,
中,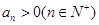 ,公比
,公比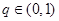 ,且
,且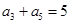 ,又
,又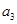 与
与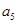 的等比中项为2.利用基本要素得到公式。
的等比中项为2.利用基本要素得到公式。
(2)由(1),得 ,∴
,∴ ,
,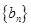 是以1为首项和公差的等差数列,∴
是以1为首项和公差的等差数列,∴ ,这就是数列
,这就是数列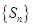 的通项公式
的通项公式
(3)由(2)知 ,裂项求和得到结论。
,裂项求和得到结论。
解:(1)∵ 的等比中项为2,∴
的等比中项为2,∴ ,又∵
,又∵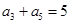 ,且
,且
∴ ,∴
,∴ ,∴
,∴ ………………4分
………………4分
(2)由(1),得 ,∴
,∴ ,
,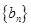 是以1为首项和公差的等差数列,∴
是以1为首项和公差的等差数列,∴ ,这就是数列
,这就是数列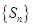 的通项公式。……8分
的通项公式。……8分
(3)由(2)知 ,
,
∴ …12分
…12分
(1)因为等比数列
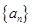 中,
中,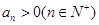 ,公比
,公比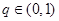 ,且
,且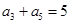 ,又
,又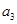 与
与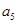 的等比中项为2.利用基本要素得到公式。
的等比中项为2.利用基本要素得到公式。(2)由(1),得
 ,∴
,∴ ,
,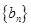 是以1为首项和公差的等差数列,∴
是以1为首项和公差的等差数列,∴ ,这就是数列
,这就是数列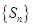 的通项公式
的通项公式(3)由(2)知
 ,裂项求和得到结论。
,裂项求和得到结论。解:(1)∵
 的等比中项为2,∴
的等比中项为2,∴ ,又∵
,又∵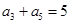 ,且
,且
∴
 ,∴
,∴ ,∴
,∴ ………………4分
………………4分(2)由(1),得
 ,∴
,∴ ,
,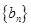 是以1为首项和公差的等差数列,∴
是以1为首项和公差的等差数列,∴ ,这就是数列
,这就是数列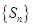 的通项公式。……8分
的通项公式。……8分(3)由(2)知
 ,
,∴
 …12分
…12分
练习册系列答案
相关题目
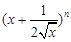 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.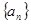 是首项
是首项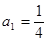 的等比数列,其前
的等比数列,其前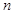 项和
项和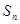 中
中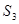 ,
,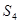 ,
,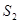 成
成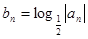 ,若
,若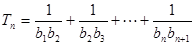 ,求证:
,求证: .
.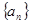 中,
中,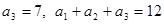 ,令
,令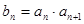 ,数列
,数列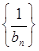 的前
的前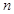 项和为
项和为 .
. ;
;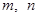 ,且
,且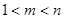 ,使得
,使得 ,
, ,
,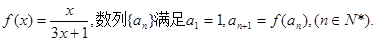
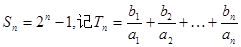 求Tn.
求Tn. 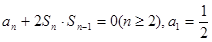
 }是等差数列;
}是等差数列;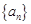 的前
的前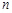 项和为
项和为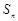 ,则
,则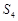 ,
,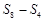 ,
,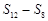 ,
,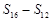 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列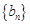 的前
的前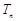 ,则
,则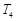 , , ,
, , ,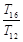 成等比数列.
成等比数列. 有n条弦的长度成等差数列,最小弦长为数列的
有n条弦的长度成等差数列,最小弦长为数列的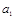 ,最大弦长为
,最大弦长为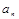 ,若公差
,若公差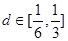 ,那么n的取值集合为( )
,那么n的取值集合为( )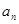 }的前
}的前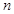 项和为
项和为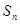 ,且
,且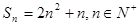 ,数列{
,数列{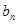 }满足
}满足 。
。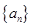 、{
、{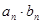 }的前
}的前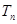 。
。