题目内容
在△ABC中,角B为锐角,已知内角A、B、C所对的边分别为a、b、c,向量
=(2sin(A+C),
),
=(cos2B,2cos2
-1),且向量
,
共线.
(1)求角B的大小;
(2)如果b=1,且S△ABC=
,求a+c的值.
| m |
| 3 |
| n |
| B |
| 2 |
| m |
| n |
(1)求角B的大小;
(2)如果b=1,且S△ABC=
| ||
| 2 |
(1)由向量
,
共线有:2sin(A+C)[2cos2
-1]=
cos2B,∴tan2B=
.
又 0<B<
,∴0<2B<π,∴2B=
,B=
.
(2)由S△ABC=
acsin
=
,得ac=2
,
由余弦定理得 b2=a2+c2-2accosB,得(a+c)2=7+4
,故a+c=2+
.
| m |
| n |
| B |
| 2 |
| 3 |
| 3 |
又 0<B<
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
(2)由S△ABC=
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 3 |
由余弦定理得 b2=a2+c2-2accosB,得(a+c)2=7+4
| 3 |
| 3 |

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
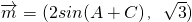 ,
,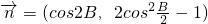 ,且向量
,且向量 共线.
共线.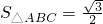 ,求a+c的值.
,求a+c的值. ,
, ,且向量
,且向量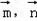 共线.
共线.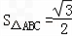 ,求a+c的值.
,求a+c的值.