题目内容
在△ABC中,角B为锐角,已知内角A、B、C所对的边分别为a、b、c,向量| m |
| 3 |
| n |
| B |
| 2 |
| m |
| n |
(1)求角B的大小;
(2)如果b=1,且S△ABC=
| ||
| 2 |
分析:(1)利用两个向量共线的性质求出tan2B的值,结合B的范围,求出2B的大小,可得B的值.
(2)根据三角形的面积求出ac=2
,由余弦定理得 (a+c)2=7+4
,求出a+c的值.
(2)根据三角形的面积求出ac=2
| 3 |
| 3 |
解答:解:(1)由向量
,
共线有:2sin(A+C)[2cos2
-1]=
cos2B,∴tan2B=
.
又 0<B<
,∴0<2B<π,∴2B=
,B=
.
(2)由S△ABC=
acsin
=
,得ac=2
,
由余弦定理得 b2=a2+c2-2accosB,得(a+c)2=7+4
,故a+c=2+
.
| m |
| n |
| B |
| 2 |
| 3 |
| 3 |
又 0<B<
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
(2)由S△ABC=
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| 3 |
由余弦定理得 b2=a2+c2-2accosB,得(a+c)2=7+4
| 3 |
| 3 |
点评:本题考查两个向量共线的性质,余弦定理的应用,求出角B是解题的难点.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
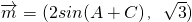 ,
,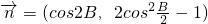 ,且向量
,且向量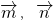 共线.
共线.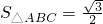 ,求a+c的值.
,求a+c的值. ,
, ,且向量
,且向量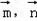 共线.
共线.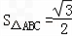 ,求a+c的值.
,求a+c的值.