题目内容

已知xsinα-ycosα=,+=,求证:+=1.

证明:由xsinα-ycosα=平方得

x2+y2=x2sin2α+y2cos2α-2xysinα·cosα,

    即x2cos2α+y2sin2α+2xysinα·cosα=0,

    即(xcosα+ysinα)2=0,

∴xcosα+ysinα=0.

∴tanα=-(当y≠0时).

∴sin2α====,

cos2α====.

∴=,

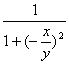    即+=1.

    当y=0时,易得+=1成立.

练习册系列答案
相关题目
已知α，β∈R，直线
x
sinα+sinβ
+
y
sinα+cosβ
=1与
x
cosα+sinβ
+
y
cosα+cosβ
=1
的交点在直线y=-x上，则sinα+cosα+sinβ+cosβ=
 
．
已知对任意平面向量
AB
=（x，y），把
AB
绕其起点沿逆时针方向旋转θ角得到向量
AP
=（xcosθ-ysinθ，xsinθ+ycosθ），叫做把点B绕点A逆时针方向旋转θ角得到点P．设平面内曲线C上的每一点绕原点沿逆时针方向旋转
π
4
后得到点的轨迹是曲线x2-y2=2，则原来曲线C的方程是
 
．
已知α，β∈R，直线
x
sinα+sinβ
+
y
sinα+cosβ
=1与
x
cosα+sinβ
+
y
cosα+cosβ
=1的交点在直线y=-x上，则sinα+cosα+sinβ+cosβ=（　　）
已知对任意平面向量
AB
=（x，y），我们把
AB
绕其起点A沿逆时针方向旋转θ角得到向量
AP
=（xcosθ-ysinθ，xsinθ+ycosθ），称为
AB
逆旋θ角到
AP
．
（1）把向量
a
=（2，-1）逆旋
π
3
角到
b
，试求向量
b
．
（2）设平面内函数y=f （x）图象上的每一点M，把
OM
逆旋
π
4
角到
ON
后（O为坐标原点），得到的N点的轨迹是曲线x2-y2=3，当函数F （x）=λ f （x）-|x-1|+2有三个不同的零点时，求实数λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网