Question

如下图所示，在矩形ABCD中，AB=4，AD=2，E是CD的中点，O为AE中点，以AE为折痕将△ADE向上折起，使D为D'，且D'B=D'C。

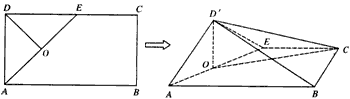
（1）求证：D'O⊥面ABCE：
（2）求OC与面D'BC所成角θ的正弦值。

Answer 1

解：（1）证明：取BC的中点F，连接OF，D'F 则OF⊥BC， 又D'B=D'C，则D'F⊥BC； ∴BC⊥面D'OF， ∴BC⊥D'O 又D'A=D'E， ∴D'O⊥AE 又AE，BC相交， ∴D'O⊥面ABCE。 （2）在平面OD'F中过O作OH⊥D'F于H，连接HC， 因为BC⊥面D'OF， ∴OH⊥BC， ∴OH⊥面D'BC， ∴HC就是OC在平面D'BC上的射影， ∴∠OCH就是OC与面D'BC所成角θ ∵AB=4，AD=2 ∴DF=3， ∴ 所以。