题目内容
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如下图所示).将矩形折叠,使A点落在线段DC上.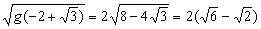
(1)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
(2)求折痕的长的最大值.
解:(1)①当k=0时,此时A点与D点重合,折痕所在的直线方程y=![]() .
.
②当k≠0时,设A点落在线段DC上的点A′(x0,1),
(0≤x0≤2),则直线OA′的斜率kOA′=![]() ,
,
∵折痕所在直线垂直平分OA′,
∴kOA′·k=-1,
∴![]() ·k=-1,∴x0=-k.
·k=-1,∴x0=-k.
又∵折痕所在的直线与OA′的交点坐标(线段OA′的中点)
为M(![]() ,
, ![]() ),
),
∴折痕所在的直线方程y-![]() =k(x+
=k(x+![]() ),即y=kx+
),即y=kx+![]() +
+![]() ,
,
由①②得折痕所在的直线方程为:y=kx+![]() +
+![]() (-2≤k≤0).
(-2≤k≤0).
(2)折痕所在的直线与坐标轴的交点坐标为E(0,![]() ),F(
),F(![]() ,0).
,0).
由(1)知,k=-x0,
∵0≤x0≤2,∴-2≤k≤0,
设折痕长度为d,所在直线的倾斜角为θ,
①当k=0时,此时A点与D点重合,折痕的长为2;
②当-2≤k<0时,
设a=![]() ,b=
,b=![]() ,
,
0<a≤|AB|=2时,l与线段AB相交,此时-2≤k≤-2+![]() ,
,
a>|AB|=2时,l与线段BC相交,此时-2+![]() <k<0,
<k<0,
0<b≤1时,l与线段AD相交,此时-1≤k<0,
b>1时,l与线段DC相交,此时-2≤k<-1,
∴将k所在的区间分为3个子区间:
a.当-2≤k<-1时,折痕所在的直线l与线段DC、AB相交,
折痕的长d=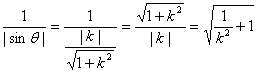 ,
,
∴![]() ≤d<
≤d<![]() ,
,
b.当-1≤k≤-2+![]() 时,折痕所在的直线l与线段AD、AB相交,
时,折痕所在的直线l与线段AD、AB相交,
折痕的长d=![]() ,
,
令g′(x)≥0,即k3+![]() ≥0,
≥0,
即2k6+3k4-1≤0,
即(k2+1)2(k2-![]() )≤0.
)≤0.
∵-1≤k≤-2+![]() ,
,
∴解得![]() ≤k≤-2+
≤k≤-2+![]() ,
,
令g′(x)≤0,解得-1≤k≤![]() ,
,
故当-1≤k≤![]() 时,g(x)是减函数;当
时,g(x)是减函数;当![]() ≤k≤-2+
≤k≤-2+![]() 时,g(x)是增函数,
时,g(x)是增函数,
∵g(-1)=2,g(-2+![]() )=4(8-4
)=4(8-4![]() ),
),
∴g(-1)<g(-2+![]() ),
),
∴当k=-2+![]() 时,g(-2+
时,g(-2+![]() )=4(8-4
)=4(8-4![]() ).
).
d=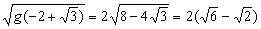 .
.
∴当-1≤k≤-2+![]() 时,d≤
时,d≤![]() ;
;
c.当-2+![]() <k<0时,折痕所在的直线l与线段AD、BC相交,
<k<0时,折痕所在的直线l与线段AD、BC相交,
折痕的长d=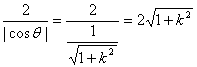 ,
,
∴2<l<![]() ,即2<l<2(
,即2<l<2(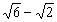 ),
),
综上所述得,当k=-2+3时,折痕的长有最大值,最大值为2(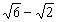 ).
).

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案